题目内容
11.函数y=lg(x2-2x)的单调增区间为( )| A. | (2,+∞) | B. | (1,+∞) | C. | (-∞,1) | D. | (-∞,2) |
分析 令t=x2-2x>0,求得函数的定义域,根据y=g(t)=lgt,本题即求函数t在定义域内的增区间,再利用二次函数的性质,得出结论.
解答 解:令t=x2-2x>0,求得x<0,或 x>2,故函数的定义域为{x|x<0,或 x>2},
根据y=g(t)=lgt,本题即求函数t在定义域内的增区间,
再利用二次函数的性质求得函数t在定义域内的增区间为(2,+∞),
故选:A.
点评 本题主要考查复合函数的单调性,对数函数、二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
6.若对于任意的x∈[-1,0],关于x的不等式3x2+2ax+b≤0恒成立,则a2+b2-1的最小值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
16.设F1、F2分别是椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左,右焦点,P为椭圆上任一点,点M的坐标为(3,3),则|PM|-|PF2|的最小值为( )
| A. | 5 | B. | $\sqrt{13}$ | C. | 1 | D. | $-\sqrt{13}$ |
3.函数y=2x2-4x-3,(0<x<3)的值域为( )
| A. | (-3,3) | B. | (-5,-3) | C. | (-5,3) | D. | (-5,+∞) |
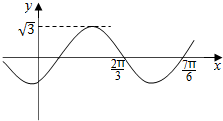 已知函数y=Asin(wx+j)(A>0,w>0,|j|<$\frac{π}{2}$)的图象如图所示,则A=$\sqrt{3}$,w=2,j=$-\frac{π}{3}$.
已知函数y=Asin(wx+j)(A>0,w>0,|j|<$\frac{π}{2}$)的图象如图所示,则A=$\sqrt{3}$,w=2,j=$-\frac{π}{3}$.