题目内容
7．
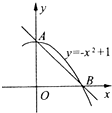如图，设抛物线y=-x2+1的顶点为A，与x轴正半轴的交点为B，设抛物线与两坐标轴正半轴围成的区域为M，随机往M内投一点，则点P落在△AOB内的概率是$\frac{3}{4}$．
分析 首先分别求出区域M和△AOB的面积，利用几何概型公式解答．
解答 解：由已知区域M的面积为${∫}_{0}^{1}（-{x}^{2}+1）dx=（-\frac{1}{3}{x}^{3}+x）{|}_{0}^{1}$=$\frac{2}{3}$，△AOB的面积为$\frac{1}{2}×OA×OB=\frac{1}{2}×1×1$=$\frac{1}{2}$，
由几何概型可得点P落在△AOB内的概率是$\frac{\frac{1}{2}}{\frac{2}{3}}=\frac{3}{4}$；
故答案为：$\frac{3}{4}$．
点评 本题考查了定积分以及几何概型公式的运用；关键是分别求出两个区域的面积，利用定积分解答．
练习册系列答案
期末集结号系列答案
相关题目
17．已知f（x）=sin（ωx+$\frac{π}{6}$）．（ω＞0），y=f（x）+1的图象与y=2的图象的两相邻交点间的距离为π，要得到y=f（x）的图象，只须把y=sinωx的图象（ ）
| A． | 向右平移$\frac{π}{12}$个单位 | B． | 向右平移$\frac{π}{6}$个单位 | ||
| C． | 向左平移$\frac{π}{12}$个单位 | D． | 向左平移$\frac{π}{6}$个单位 |
12．设点P在曲线y=x2+1（x≥0）上，点Q在曲线y=$\sqrt{x-1}$（x≥1）上，则|PQ|的最小值为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{3\sqrt{2}}{4}$ | C． | $\sqrt{2}$ | D． | $\frac{3\sqrt{2}}{2}$ |