题目内容

已知点P（a，b）与点Q（1，0）在直线2x-3y+1=0的两侧，则下列说法正确的序号是
③④
③④

①2a-3b+1＞0
②a≠0时，
b
a
有最小值，无最大值
③a＞0且a≠1，b＞0，
b
a-1
的取值范围为（-∞，-
1
3
）∪（
2
3
，+∞）
④存在正实数M，使
a2+b2
＞M恒成立．
分析：由已知点P（a，b）与点Q（1，0）在直线2x-3y+1=0的两侧可得2a-3b+1＜0，结合不等式的性质可得当a＞0时，
b
a
＞
2
3
+
1
3a
，从而对①②作出判断；对于③，利用式子蕴含的斜率的几何意义即可解决．对于④，是看
a2+b2
有没有极小值，据
a2+b2
的几何意义即可得出；
解答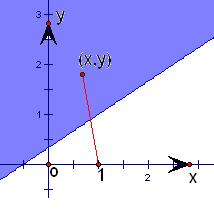：解：①由已知（2a-3b+1）（2-0+1）＜0，即2a-3b+1＜0，∴①错；
②当a＞0时，由3b＞2a+1，可得
b
a
＞
2
3
+
1
3a
，∴不存在最小值，
∴②错；
③∵
b
a-1
表示点（a，b）与点（1，0）连线的斜率，
如图，由线性规划知识可知，当a＞0，b＞0时，
b
a-1
的取值范围为：
（-∞，-
1
3
）∪（
2
3
，+∞）．③正确．
④
a2+b2
表示为（a，b）与（0，0）两点间的距离，
由于原点（0，0）到直线2x-3y+1=0的距离d=
1
4+9
，
由此可得：
a2+b2
＞
1
4+9
=
13
13
恒成立，∴④正确；
故答案是：③④．
点评：本题主要考查了简单线性规划，用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．
练习册系列答案
相关题目
给出以下四个结论：
（1）函数f(x)=
x-1
x+1
的对称中心是（-1，-1）；
（2）若关于x的方程x-
1
x
+k=0在x∈（0，1）没有实数根，则k的取值范围是k≥2
（3）已知点P（a，b）与点Q（1，0）在直线2x-3y+1=0两侧，则3b-2a＞1；
（4）若将函数f(x)=sin(2x-
π
3
)的图象向右平移?（?＞0）个单位后变为偶函数，则?的最小值是
π
12
其中正确的结论是：
 
．
给出以下四个结论：
（1）函数f(x)=
x-1
2x+1
的对称中心是(-
1
2
，-
1
2
)；
（2）若关于x的方程x-
1
x
+k=0在x∈（0，1）没有实数根，则k的取值范围是k≥2；
（3）已知点P（a，b）与点Q（1，0）在直线2x-3y+1=0两侧，当a＞0且a≠1，b＞0时，
b
a-1
的取值范围为(-∞，-
1
3
)∪(
2
3
，+∞)；
其中正确的结论是：
 
．
给出以下五个结论：
（1）函数f(x)=
x-1
2x+1
的对称中心是(-
1
2
，-
1
2
)；
（2）若关于x的方程x-
1
x
+k=0在x∈（0，1）没有实数根，则k的取值范围是k≥2；
（3）已知点P（a，b）与点Q（1，0）在直线2x-3y+1=0两侧，当a＞0且a≠1，b＞0时，
b
a-1
的取值范围为(-∞，-
1
3
)∪(
2
3
，+∞)；
（4）若将函数f(x)=sin(2x-
π
3
)的图象向右平移?（?＞0）个单位后变为偶函数，则?的最小值是
5π
12
；
（5）已知m，n是两条不重合的直线，α，β是两个不重合的平面，若m⊥α，n∥β且m⊥n，则α⊥β；其中正确的结论是：
 
．
（2011•福建模拟）给出以下四个结论：
（1）若关于x的方程x-
1
x
+k=0在x∈（0，1）没有实数根，则k的取值范围是k≥2
（2）曲线y=1+
4-x2
(|x|≤2)与直线y=k（x-2）+4有两个交点时，实数k的取值范围是(
5
12
，
3
4
]
（3）已知点P（a，b）与点Q（1，0）在直线2x-3y+1=0两侧，则3b-2a＞1；
（4）若将函数f(x)=sin(2x-
π
3
)的图象向右平移?（?＞0）个单位后变为偶函数，则?的最小值是
π
12
，其中正确的结论是：
（2）（3）（4）
（2）（3）（4）
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网