题目内容
 如图,梯形ABCD中,CD∥AB,AD=DC=CB=
如图,梯形ABCD中,CD∥AB,AD=DC=CB=| 1 | 2 |
(1)求证:DE⊥PC;
(2)求点D到平面PBC的距离;
(3)求二面角D-PC-B的大小.
分析:(1)四边形ADCE是菱形,连接AC交DE于F,连接PF,则DE⊥AC,DE⊥PF,AC∩PF=F,根据直线与平面垂直的判定定理可知,DE⊥平面PFC,又PC?平面PFC,则DE⊥PC.
(2)利用线面平行进而把点D转化为点F到面得距离,在利用面面垂直得到垂足的位置,然后在三角形中解出所求线段的长度.
(3)利用二面角的平面角定义找到二面角的平面角,然后在Rt△DHO中解出二面角的大小即可;
(2)利用线面平行进而把点D转化为点F到面得距离,在利用面面垂直得到垂足的位置,然后在三角形中解出所求线段的长度.
(3)利用二面角的平面角定义找到二面角的平面角,然后在Rt△DHO中解出二面角的大小即可;
解答:解:(1)连接EC,
∵E是AB的中点,∴BE=
AB,
又∵CD∥AB,DC=
AB,∴DC∥EB且DC=EB
∴CD∥AE且CD=AE,
∴四边形ADCE为平行四边形,
又AD=DC,∴四边形ADCE是菱形.
连接AC交DE于F,连接PF,
则DE⊥AC,DE⊥PF,
∵AC∩PF=F,∴DE⊥平面PFC.
又∵PC?平面PFC,∴DE⊥PC.
( 2)∵DE∥BC,DE在平面PBC外,
∴DE∥面PBC,∴D点到面PBC的距离即为点F到面PBC的距离,过点F作FG⊥PC,垂足为G,
∵DE⊥面PCF,∴BC⊥面PCF∴面PBC⊥面PCF,∴FG⊥面PBC,
∴FG的长即为点F到面PBC的距离,菱形ADCE中,AF=FC,
∴PF=CF=
a,∵∠PFC=120°,∴∠FPC=∠FCP=30°,
∴FG=
PF=
a
(3)取PB的中点G,连HG,可知∠DHG为所求二面角,DO=HG=
a,DH=
a,
在直角三角形DHO中,sin∠DHO=
=
,又因为GH⊥面POC,
∴GH⊥OH∠DHG=∠DHO+∠GHO=
+arcsin
.
(或∠DHG=π-arctan
=π-arccos
).
∵E是AB的中点,∴BE=
| 1 |
| 2 |
又∵CD∥AB,DC=
| 1 |
| 2 |
∴CD∥AE且CD=AE,
∴四边形ADCE为平行四边形,
又AD=DC,∴四边形ADCE是菱形.
连接AC交DE于F,连接PF,
则DE⊥AC,DE⊥PF,
∵AC∩PF=F,∴DE⊥平面PFC.
又∵PC?平面PFC,∴DE⊥PC.
( 2)∵DE∥BC,DE在平面PBC外,
∴DE∥面PBC,∴D点到面PBC的距离即为点F到面PBC的距离,过点F作FG⊥PC,垂足为G,
∵DE⊥面PCF,∴BC⊥面PCF∴面PBC⊥面PCF,∴FG⊥面PBC,
∴FG的长即为点F到面PBC的距离,菱形ADCE中,AF=FC,
∴PF=CF=
| ||
| 2 |
∴FG=
| 1 |
| 2 |
| ||
| 4 |
(3)取PB的中点G,连HG,可知∠DHG为所求二面角,DO=HG=
| 1 |
| 2 |
| ||
| 4 |
在直角三角形DHO中,sin∠DHO=
| DO |
| DH |
2
| ||
| 7 |
∴GH⊥OH∠DHG=∠DHO+∠GHO=
| π |
| 2 |
2
| ||
|
(或∠DHG=π-arctan
| ||
| 2 |
2
| ||
| 7 |
点评:本题考查直线与平面平行的判定,直线与平面所成的角的求法,考查学生空间想象能力,逻辑思维能力,把要求的点到面得距离转化为易求的点到面得距离,并利用面面垂直找到点在面内的垂足的位置,此外还考查了学生利用反三角函数的知识表示角的大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
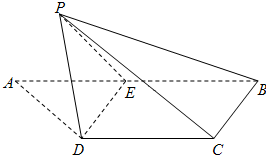 如图,梯形ABCD中,CD∥AB,AD=DC=CB=
如图,梯形ABCD中,CD∥AB,AD=DC=CB= 如图,梯形ABCD中,AD∥BC,PA⊥平面ABCD,E是PD的中点,AB=BC=1,PA=AD=2.
如图,梯形ABCD中,AD∥BC,PA⊥平面ABCD,E是PD的中点,AB=BC=1,PA=AD=2.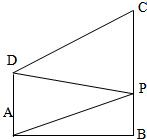 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是BC上的动点,当
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是BC上的动点,当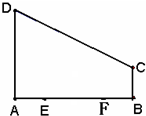 如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.
如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.