题目内容
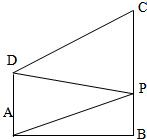 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是BC上的动点,当
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是BC上的动点,当| PD |
| PA |
分析:由余弦定理可得 1=AP2+DP2-2
•
,即
•
=
,利用基本不等式可得当
•
最小时,点P是AD的中垂线和BC的交点,tan
=
=
,利用倍角的正切公式求得tan∠APD 的值.
| PD |
| PA |
| PD |
| PA |
| AP2 +DP2-1 |
| 2 |
| PD |
| PA |
| ∠APD |
| 2 |
| ||
| 3 |
| 1 |
| 6 |
解答:解:∵
•
=PD•PA cos∠APD,△PDA中,由余弦定理可得
1=AP2+DP2-2AP•DPcos∠APD=AP2+DP2-2
•
,
∴
•
=
≥
,当且仅当AP=DP 时,等号成立.
故当
•
最小时,点P是AD的中垂线和BC的交点,tan
=
=
,
∴tan∠APD=
=
=
,
故答案为:
.
| PD |
| PA |
1=AP2+DP2-2AP•DPcos∠APD=AP2+DP2-2
| PD |
| PA |
∴
| PD |
| PA |
| AP2 +DP2-1 |
| 2 |
| 2AP•DP-1 |
| 2 |
故当
| PD |
| PA |
| ∠APD |
| 2 |
| ||
| 3 |
| 1 |
| 6 |
∴tan∠APD=
2tan
| ||
1-tan2
|
| ||
1-(
|
| 12 |
| 35 |
故答案为:
| 12 |
| 35 |
点评:本题考查余弦定理,基本不等式,二倍角的正切公式的应用,求出tan
的值,是解题的关键.
| ∠APD |
| 2 |

练习册系列答案
相关题目
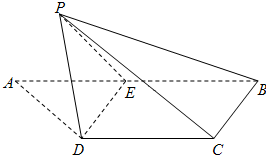 如图,梯形ABCD中,CD∥AB,AD=DC=CB=
如图,梯形ABCD中,CD∥AB,AD=DC=CB= 如图,梯形ABCD中,AD∥BC,PA⊥平面ABCD,E是PD的中点,AB=BC=1,PA=AD=2.
如图,梯形ABCD中,AD∥BC,PA⊥平面ABCD,E是PD的中点,AB=BC=1,PA=AD=2. 如图,梯形ABCD中,CD∥AB,
如图,梯形ABCD中,CD∥AB,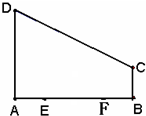 如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.
如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.