题目内容
设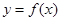 (
(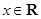 ,
,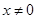 )对任意非零实数
)对任意非零实数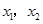 均满足
均满足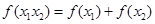 ,则
,则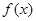 为 函数(“奇”或“偶”).
为 函数(“奇”或“偶”).
【答案】
偶
【解析】
试题分析:首先f(1×1)=f(1)+f(1) 则 f(1)=0
f((-1)×(-1))=f(-)+f(-1)=0 则 f(-1)=0
所以 f(1)=f(-1)=0
从而f(-1×x)=f(x)+f(-1) 即 f(-x)=f(x)
所以 f(x)是偶函数
考点:本题主要考查抽象函数奇偶性的判断。
点评:常见题,此类问题常常利用“赋值法”。

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
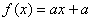 和反比例函数
和反比例函数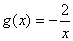 的反函数分别是
的反函数分别是 ,若存在实常数
,若存在实常数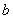 使得对任意非零实数
使得对任意非零实数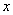 ,
,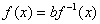 和
和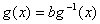 都成立.
都成立.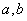 的值;
的值;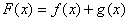 ,试判断函数
,试判断函数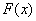 在
在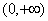 上的单调性并证明.
上的单调性并证明.