Question

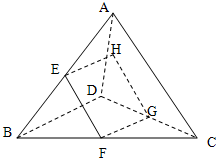已知空间四边形ABCD中，E、H分别为AB、AD的中点，F、G分别为BC、CD的中点．
（1）求证：四边形EFGH为平行四边形；
（2）若平行四边形EFGH为菱形，判断线段AC与线段BD的大小关系．

Answer 1

分析：（1）根据空间直线平行的性质即可证明四边形EFGH为平行四边形；
（2）根据平行四边形EFGH为菱形，即可判断线段AC与线段BD的大小关系．

解答：解：（1）∵E、H分别为AB、AD的中点，F、G分别为BC、CD的中点．
∴EH∥BD，且EH=

1

2

BD，
FG∥BD，且FG=

1

2

BD，
即EH∥FG，且EH=FG，
即四边形EFGH为平行四边形；
（2）若平行四边形EFGH为菱形，
则EH=EF，
∵E，F分别是AB，BC的中点，
∴EF∥AC，且EF=

1

2

AC，
又FG=

1

2

BD，
∴AC=BD．

点评：本题主要考查空间直线的位置关系的判断，利用中位线的性质是解决本题的根据，要求熟练掌握直线平行的平行公理的应用．