题目内容
18．
抛物线x2=y（-2≤x≤2）绕轴旋转180°形成一个如图所示的旋转体，在此旋转体内水平放入一个正方体，使正方体的上底面恰好与旋转体的开口面平齐，下底面的四个顶点落在曲面上，则此正方体的外接球的表面积为（ ）| A． | 4π | B． | 12π | C． | 16π | D． | 48π |
分析 由题意画出过正方体的两条相对侧棱的截面图，设出正方体的棱长，然后利用A点的纵坐标相等列式求解a的值，可得正方体的棱长是2，求出正方体的外接球的半径，即可求出正方体的外接球的表面积．
解答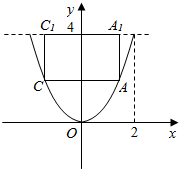 
解：作过正方体的两条相对侧棱的截面图如图，
设正方体AC1的棱长AA1=a，则底面对角线AC=$\sqrt{2}$a，
所以A点的横坐标等于$\frac{\sqrt{2}a}{2}$，代入抛物线y=x2得A点纵坐标为$\frac{{a}^{2}}{2}$．
又由题意可知A点纵坐标等于4-a．
所以$\frac{{a}^{2}}{2}$=4-a，解得：a=2．
所以正方体的棱长是2，
所以正方体的外接球的半径为$\sqrt{3}$，
所以正方体的外接球的表面积为4π•3=12π．
故选：B．
点评 本题考查了抛物线的应用，考查了数形结合的解题思想和数学转化思想，能够正确作出该题的截面图是解答该题的关键，属中档题．
练习册系列答案
相关题目
9．在△ABC中，下列式子与$\frac{sinA}{a}$的值相等的是（ ）
| A． | $\frac{b}{c}$ | B． | $\frac{sinB}{sinA}$ | C． | $\frac{sinC}{c}$ | D． | $\frac{c}{sinC}$ |
6．在区间（-5，5）内随机地取出一个实数a，使得不等式2+a-a2＞0成立的概率是（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{3}{10}$ | C． | $\frac{5}{10}$ | D． | $\frac{7}{10}$ |
10．某学校组织高一高二两个年级的50名学生干部利用假期参加社会实践活动，活动内容是：①到社会福利院慰问孤寡老人；②到车站做义工，帮助需要帮助的旅客．各位同学根据各自的实际情况，选择了不同的活动项目，相关的数据如下表所示：
（1）用分层抽样的方法在到车站做义工的同学中随机抽取6名，求在高二年级的学生中应抽取几名？
（2）在（1）中抽取的6名同学中任取2名，求选到的同学为高二年级学生人数的数学期望；
（3）如果“到社会福利院慰问老人”与“到车站做义工”是两个分类变量，并且计算出随机变量K2=2.981，那么，你有多大把握认为选择到社会福利院慰问老人与到车站做义工是与年级有关系的？
| 到社会福利院慰问老人 | 到车站做义工 | 总计 | |
| 高一 | 11 | 16 | 27 |
| 高二 | 15 | 8 | 23 |
| 总计 | 26 | 24 | 50 |
（2）在（1）中抽取的6名同学中任取2名，求选到的同学为高二年级学生人数的数学期望；
（3）如果“到社会福利院慰问老人”与“到车站做义工”是两个分类变量，并且计算出随机变量K2=2.981，那么，你有多大把握认为选择到社会福利院慰问老人与到车站做义工是与年级有关系的？
| 参考数据 | P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
7．已知a，b，c，d成等比数列，且曲线y=x2-2x+3的顶点坐标为（b，d），则a+c=（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{3\sqrt{2}}{2}$ | C． | -$\frac{3\sqrt{2}}{2}$ | D． | ±$\frac{3\sqrt{2}}{2}$ |