题目内容
(2012•临川区模拟)请考生在下列两题中任选一题作答.若两题都做,则按做的第一题评阅计分.
(1)已知曲线C1、C2的极坐标方程分别为ρ=-2cos(θ+
),
ρcos(θ-
)+1=0,则曲线C1上的点与曲线C2上的点的最远距离为
+1
+1.
(2)设a=
,b=p
,c=x+y,若对任意的正实数x,y,都存在以a,b,c为三边长的三角形,则实数p的取值范围是
(1)已知曲线C1、C2的极坐标方程分别为ρ=-2cos(θ+
| π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| 2 |
(2)设a=
| x2-xy+y2 |
| xy |
(1,3)
(1,3)
.分析:(1)先将曲线的极坐标方程方程化为普通方程,曲线C1的普通方程为x2+y2=2y,即x2+(y-1)2=1.表示以C(0,1)为圆心,半径为1 的圆.曲线C2的普通方程为x+y+1=0,表示一条直线.利用直线和圆的位置关系求解.
(2)由基本不等式可得a≥
,c≥2
,再由三角形任意两边之和大于第三边可得,
+2
>b=p
,且p
+
>2
,p
+2
>
,由此求得实数p的取值范围.
(2)由基本不等式可得a≥
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
解答: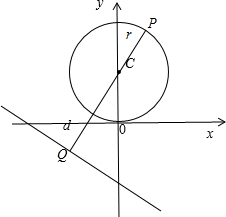 曲线C1极坐标方程为ρ=-2cos(θ+
曲线C1极坐标方程为ρ=-2cos(θ+
),即ρ=2sinθ,ρ2=2ρsinθ
化为直角坐标方程为x2+y2-2y=0.即x2+(y-1)2=1.
表示以C(0,1)为圆心,半径为1 的圆.
C2的极坐标方程为,
ρcos(θ-
)+1=0,即
ρ(
cosθ+
sinθ)+1=0,
化为普通方程为x+y+1=0,表示一条直线
如图,圆心到直线距离d=|CQ|=
,曲线C1上的点与曲线C2上的点的最远距离为|PQ|=d+r=
+1
(2)对于正实数x,y,由于a=
≥
=
,c=x+y≥2
,b=p
,且三角形任意两边之和大于第三边,所以
+2
>b=p
,且p
+
>2
,p
+2
>
,.
解得 1<p<3,故实数p的取值范围是(1,3),
故答案为:
+1,(1,3).
 曲线C1极坐标方程为ρ=-2cos(θ+
曲线C1极坐标方程为ρ=-2cos(θ+| π |
| 2 |
化为直角坐标方程为x2+y2-2y=0.即x2+(y-1)2=1.
表示以C(0,1)为圆心,半径为1 的圆.
C2的极坐标方程为,
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
化为普通方程为x+y+1=0,表示一条直线
如图,圆心到直线距离d=|CQ|=
| 2 | ||
|
| 2 |
| 2 |
(2)对于正实数x,y,由于a=
| x2-xy+y2 |
| 2xy -xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
| xy |
解得 1<p<3,故实数p的取值范围是(1,3),
故答案为:
| 2 |
点评:(1)本题以曲线参数方程出发,考查了极坐标方程、普通方程间的互化,直线和圆的位置关系.(2)本题主要考查基本不等式的应用,注意不等式的使用条件,以及三角形中任意两边之和大于第三边,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目