题目内容
已知抛物线P:x2=2py (p>0).(Ⅰ)若抛物线上点M(m,2)到焦点F的距离为3.
(ⅰ)求抛物线P的方程;
(ⅱ)设抛物线P的准线与y轴的交点为E,过E作抛物线P的切线,求此切线方程;
(Ⅱ)设过焦点F的动直线l交抛物线于A,B两点,连接AO,BO并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
【答案】分析:(Ⅰ)(ⅰ)欲求抛物线方程,需求出p值,根据抛物线上点到焦点F的距离与到准线距离相等,以及抛物线上点M(m,2)到焦点F的距离为3,可解得 p,问题得解.
(ⅱ)求出E点坐标,设出过E的抛物线P的切线方程,再根据直线方程与抛物线方程联立,△=0,即可求出k值,进而求出切线方程.
(Ⅱ)设出A,B两点坐标,以及过焦点F的动直线l方程,代入抛物线方程,求x1x2,x1+x2,再求C,D点坐标,用含x1,x2的式子表示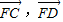 坐标,在证
坐标,在证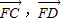 共线即可.
共线即可.
解答:解:(Ⅰ)(ⅰ)由抛物线定义可知,抛物线上点M(m,2)到焦点F的距离与到准线距离相等,
即M(m,2)到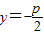 的距离为3;
的距离为3;
∴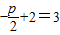 ,解得p=2.
,解得p=2.
∴抛物线P的方程为x2=4y.
(ⅱ)抛物线焦点F(0,1),抛物线准线与y轴交点为E(0,-1),
显然过点E的抛物线的切线斜率存在,设为k,切线方程为y=kx-1.
由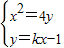 ,消y得x2-4kx+4=0,
,消y得x2-4kx+4=0,
△=16k2-16=0,解得k=±1.
∴切线方程为y=±x-1.
(Ⅱ)直线l的斜率显然存在,设l: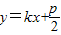 ,
,
设A(x1,y1),B(x2,y2),
由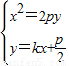 消y得 x2-2pkx-p2=0. 且△>0.
消y得 x2-2pkx-p2=0. 且△>0.
∴x1+x2=2pk,x1•x2=-p2;
∵A(x1,y1),∴直线OA: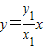 ,
,
与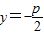 联立可得
联立可得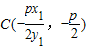 ,同理得
,同理得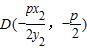 .
.
∵焦点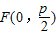 ,
,
∴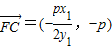 ,
, ,
,
∴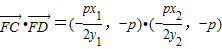 =
=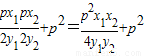 =
=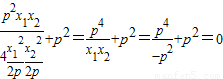
∴以CD为直径的圆过焦点F.
点评:本题考查了抛物线方程的求法,以及直线与抛物线的位置关系判断,做题时要认真分析,避免不必要的错误.
(ⅱ)求出E点坐标,设出过E的抛物线P的切线方程,再根据直线方程与抛物线方程联立,△=0,即可求出k值,进而求出切线方程.
(Ⅱ)设出A,B两点坐标,以及过焦点F的动直线l方程,代入抛物线方程,求x1x2,x1+x2,再求C,D点坐标,用含x1,x2的式子表示
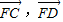 坐标,在证
坐标,在证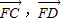 共线即可.
共线即可.解答:解:(Ⅰ)(ⅰ)由抛物线定义可知,抛物线上点M(m,2)到焦点F的距离与到准线距离相等,
即M(m,2)到
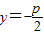 的距离为3;
的距离为3;∴
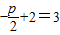 ,解得p=2.
,解得p=2.∴抛物线P的方程为x2=4y.
(ⅱ)抛物线焦点F(0,1),抛物线准线与y轴交点为E(0,-1),
显然过点E的抛物线的切线斜率存在,设为k,切线方程为y=kx-1.
由
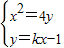 ,消y得x2-4kx+4=0,
,消y得x2-4kx+4=0,△=16k2-16=0,解得k=±1.
∴切线方程为y=±x-1.
(Ⅱ)直线l的斜率显然存在,设l:
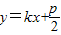 ,
,设A(x1,y1),B(x2,y2),
由
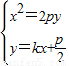 消y得 x2-2pkx-p2=0. 且△>0.
消y得 x2-2pkx-p2=0. 且△>0.∴x1+x2=2pk,x1•x2=-p2;
∵A(x1,y1),∴直线OA:
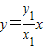 ,
,与
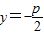 联立可得
联立可得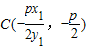 ,同理得
,同理得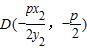 .
. ∵焦点
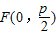 ,
,∴
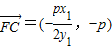 ,
, ,
,∴
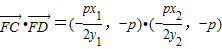 =
=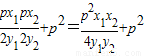 =
=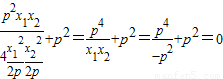
∴以CD为直径的圆过焦点F.
点评:本题考查了抛物线方程的求法,以及直线与抛物线的位置关系判断,做题时要认真分析,避免不必要的错误.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 到焦点F的距离为
到焦点F的距离为 .
. 的方程;
的方程; ,
, 并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.