题目内容
已知抛物线P:x2=2py (p>0).
(Ⅰ)若抛物线上点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
(ⅰ)求抛物线![]() 的方程;
的方程;
(ⅱ)设抛物线![]() 的准线与y轴的交点为E,过E作抛物线
的准线与y轴的交点为E,过E作抛物线![]() 的切线,求此切线方程;
的切线,求此切线方程;
(Ⅱ)设过焦点F的动直线l交抛物线于A,B两点,连接![]() ,
,![]() 并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
解:(Ⅰ)(ⅰ)由抛物线定义可知,抛物线上点![]() 到焦点F的距离与到准线距离相等,
到焦点F的距离与到准线距离相等,
即![]() 到
到![]() 的距离为3;
的距离为3;
∴ ![]() ,解得
,解得![]() .
.
∴ 抛物线![]() 的方程为
的方程为![]() . ………………4分
. ………………4分
(ⅱ)抛物线焦点![]() ,抛物线准线与y轴交点为
,抛物线准线与y轴交点为![]() ,
,
显然过点![]() 的抛物线的切线斜率存在,设为
的抛物线的切线斜率存在,设为![]() ,切线方程为
,切线方程为![]() .
.
由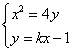 , 消y得
, 消y得![]() , ………………6分
, ………………6分
![]() ,解得
,解得![]() . ………………7分
. ………………7分
∴切线方程为![]() . ………………8分
. ………………8分
(Ⅱ)直线![]() 的斜率显然存在,设
的斜率显然存在,设![]() :
:![]() ,
,
设![]() ,
,![]() ,
,
由 消y得
消y得 ![]() . 且
. 且![]() .
.
∴ ![]() ,
,![]() ;
;
∵ ![]() , ∴ 直线
, ∴ 直线![]() :
:![]() ,
,
与![]() 联立可得
联立可得![]() , 同理得
, 同理得![]() .……………10分
.……………10分
∵ 焦点![]() ,
,
∴ ![]() ,
,![]() , ………………12分
, ………………12分
∴ ![]()
![]()
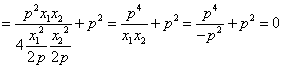
∴ 以![]() 为直径的圆过焦点
为直径的圆过焦点![]() . ………………14分
. ………………14分

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 到焦点F的距离为
到焦点F的距离为 .
. 的方程;
的方程; ,
, 并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.