题目内容
10．设数列{xn}满足0＜x1＜π，xn+1=sinxn（n=1，2，…），证明$\underset{lim}{n→∞}$xn存在极限，并求该极限．分析 0＜xn+1=sinxn≤1，可得：当n≥2时，xn+1=sinxn＜xn，数列{xn}满足单调递减且有界，因此$\underset{lim}{n→∞}$xn存在，解出即可．
解答 证明：∵0＜xn+1=sinxn≤1，
∴当n≥2时，xn+1=sinxn＜xn，
∴数列{xn}满足单调递减且有界，
因此$\underset{lim}{n→∞}$xn存在，
设$\underset{lim}{n→∞}$xn=x，
则x=sinx，
解得x=0，
∴$\underset{lim}{n→∞}$xn=0．
点评 本题考查了单调有界数列必有极限的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
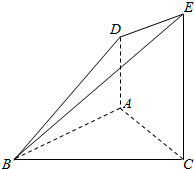如图所示，AD⊥平面ABC，CE⊥平面ABC，CE=2AD，AC=AB=1，BC=$\sqrt{2}$，证明：