题目内容
1.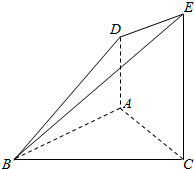 如图所示,AD⊥平面ABC,CE⊥平面ABC,CE=2AD,AC=AB=1,BC=$\sqrt{2}$,证明:
如图所示,AD⊥平面ABC,CE⊥平面ABC,CE=2AD,AC=AB=1,BC=$\sqrt{2}$,证明:(1)AB⊥平面ACED;
(2)平面BDE⊥平面BCE.
分析 (1)证明AB⊥AC,AD⊥AB,即可证明AB⊥平面ACED;
(2)由AB=AC,F为BC的中点可得AF⊥BC,结合GF⊥AF及线面垂直的判定定理可得AF⊥平面BCE进而由面面垂直的判定定理得到平面BDE⊥平面BCE.
解答  证明:(1)∵AC=AB=1,BC=$\sqrt{2}$,
证明:(1)∵AC=AB=1,BC=$\sqrt{2}$,
∴AB⊥AC,
∵AD⊥平面ABC,AB?平面ABC,
∴AD⊥AB,
∵AD∩AC=A,
∴AB⊥平面ACED;
(2)设F为BC的中点,作BE的中点G,连接GF,GD
∵AB=AC,F为BC的中点,
∴AF⊥BC,又GF⊥AF,∴AF⊥平面BCE,
∵AF∥GD,∴GD⊥平面BCE,
又GD?平面BDE,
∴平面BDE⊥平面BCE.
点评 本题考查直线与平面、平面与平面垂直的判定,正确证明线面垂直是关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
6.已知数列{an}的通项公式为an =n2+1,则该数列的第6项是( )
| A. | 37 | B. | 36 | C. | 26 | D. | 7 |
 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示:
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示: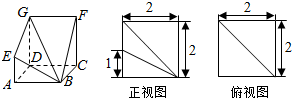 如图,多面体ABCD-EGF中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图,俯视图及相关数据如图.
如图,多面体ABCD-EGF中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图,俯视图及相关数据如图.