题目内容
在平面直角坐标系xOy中,已知△ABC的顶点A,B的坐标分别为A(-3,0),B(3,0),△ABC的周长为16,
(Ⅰ)求顶点C的轨迹方程;
(Ⅱ)过点A作直线,与(Ⅰ)中的曲线交于M,N两点,试判断 是否存在最小值,若存在,求出最小值;若不存在,请说明理由。
是否存在最小值,若存在,求出最小值;若不存在,请说明理由。
(Ⅰ)求顶点C的轨迹方程;
(Ⅱ)过点A作直线,与(Ⅰ)中的曲线交于M,N两点,试判断
 是否存在最小值,若存在,求出最小值;若不存在,请说明理由。
是否存在最小值,若存在,求出最小值;若不存在,请说明理由。 解:(Ⅰ)∵|CA|+|CB|=10为定值,
所以C点的轨迹是以A,B为焦点的椭圆,焦距2c=6,
设椭圆为方程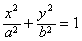 ,且2a=10,
,且2a=10,
易得a=5,c=3,b=4,
所以C点的轨迹方程为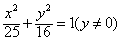 。
。
(Ⅱ)设M(x1,y1),N(x2,y2),
当直线MN的倾斜角不为90°时,设其方程为y=k(x+3)(k≠0),
代入椭圆方程化简,得 ,
,
显然有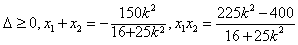 ,
,
又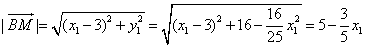 ,
,
同理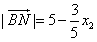 ,
,
所以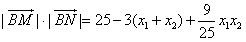
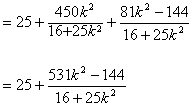
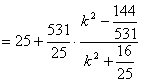 ,
,
只要考虑 的最小值,即考虑
的最小值,即考虑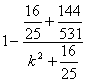 取最小值,
取最小值,
而k≠0,所以上式无最小值,
显然k=0时,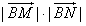 取最小值16;
取最小值16;
当直线MN的倾斜角为90°时,x1=x2=-3,
得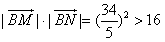 ;
;
∴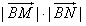 的最小值不存在。
的最小值不存在。
所以C点的轨迹是以A,B为焦点的椭圆,焦距2c=6,
设椭圆为方程
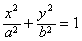 ,且2a=10,
,且2a=10,易得a=5,c=3,b=4,
所以C点的轨迹方程为
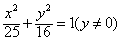 。
。(Ⅱ)设M(x1,y1),N(x2,y2),
当直线MN的倾斜角不为90°时,设其方程为y=k(x+3)(k≠0),
代入椭圆方程化简,得
 ,
,显然有
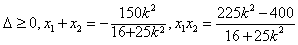 ,
,又
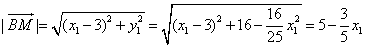 ,
,同理
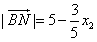 ,
,所以
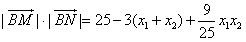
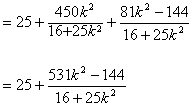
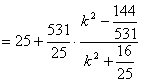 ,
,只要考虑
 的最小值,即考虑
的最小值,即考虑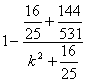 取最小值,
取最小值,而k≠0,所以上式无最小值,
显然k=0时,
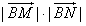 取最小值16;
取最小值16;当直线MN的倾斜角为90°时,x1=x2=-3,
得
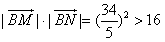 ;
;∴
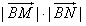 的最小值不存在。
的最小值不存在。
练习册系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.