题目内容
.已知函数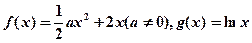 .
.
(1)若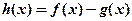 存在单调增区间,求
存在单调增区间,求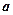 的取值范围;
的取值范围;
(2)是否存在实数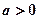 ,使得方程
,使得方程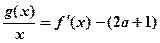 在区间
在区间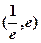 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出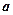 的取值范围?若不存在,请说明理由。
的取值范围?若不存在,请说明理由。
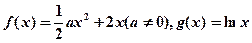 .
.(1)若
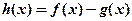 存在单调增区间,求
存在单调增区间,求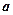 的取值范围;
的取值范围;(2)是否存在实数
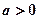 ,使得方程
,使得方程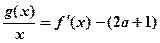 在区间
在区间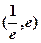 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出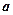 的取值范围?若不存在,请说明理由。
的取值范围?若不存在,请说明理由。解:(1)由已知,得h(x)=
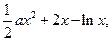 且x>0, 则hˊ(x)=ax+2-
且x>0, 则hˊ(x)=ax+2-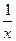 =
=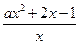 ,
, ∵函数h(x)存在单调递增区间, ∴hˊ(x) > 0有解, 即不等式ax2+2x-1>0有解. (2分)
① 当a<0时, y=ax2+2x-1的图象为开口向下的抛物线, 要使ax2+2x-1>0总有解,只需Δ="4+4a>0," 即a>-1. 即-1<a<0
② 当a>0 时, y= ax2+2x-1的图象为开口向上的抛物线, ax2+2x-1>0 一定有解.
综上, a的取值范围是(-1, 0)∪(0, +∞) (5分)
(2)方程
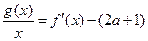

解得
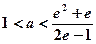 ,所以
,所以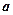 的取值范围是
的取值范围是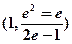 (12分)
(12分)略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
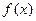 的单调区间;
的单调区间;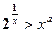 对任意
对任意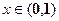 恒成立,求实数
恒成立,求实数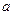 的取值范围.
的取值范围.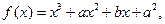 在
在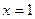 时有极值
时有极值 ,那么
,那么 的
的 值分别为 。
值分别为 。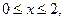 ,求函数
,求函数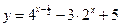 的最大值,最小值。
的最大值,最小值。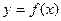 在定义域内可导,已知
在定义域内可导,已知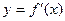 的图象为
的图象为 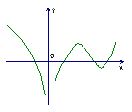
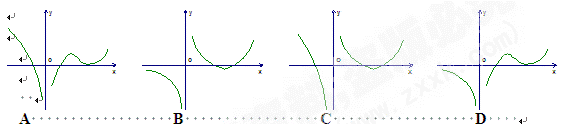
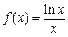 ,在区间[2,3]上任取一点
,在区间[2,3]上任取一点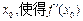 >0的概率为
>0的概率为  。
。