题目内容
设定义域在R上的函数f(x)=a0x4+a1x3+a2x2+a3x,(ai∈R,i=0,1,2,3),当x=-(1)求f(x)的解析式;
(2)试在函数f(x)的图像上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间[-1,1]上;
(3)求证:|f(sinx)-f(cosx)|≤![]() ,(x∈R).
,(x∈R).
解:(1)∵f′(x)=4a0x3+3a1x2+2a1x+a3
由于f′(x)为偶函数 ∴a0=a1=0
∴f(x)=a1x3+a3x,f′(x)=3a1x2+a3
又∵x=-![]() 时,f(x)取得极大值
时,f(x)取得极大值![]()
∴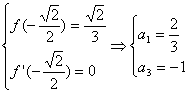
即f(x)=![]() x3-x.
x3-x.
(2)设所求点的横坐标为x1、x2(x1<x2)
由已知这两点处切线斜率为![]()
∵(![]() )·(
)·(![]() )=-1
)=-1
∵x1、x2∈[-1,1]. ∴![]() ∈[-1,1]
∈[-1,1]
存在![]() 中有一个为1,另一个为-1.
中有一个为1,另一个为-1.
∴
∴所求两点坐标为 (0,0)与(1,![]() )或(0,0)与(-1,
)或(0,0)与(-1,![]() )
)
(3) ∵sinx,cosx∈[-1,1]
而f′(x)=2x2-1=0![]() x=±
x=±![]()
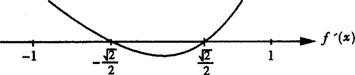
∴f(x)在[-1,![]() ]及[
]及[![]() ,1]上递减,
,1]上递减,
在[-![]() ,
,![]() ]上递减
]上递减
即f(x)极大值=f(-![]() )=
)=![]()
f(x)极小值=f(![]() )=-
)=-![]()
而f(-1)=![]() f(-1)=-
f(-1)=-![]()
∴f(x)max=![]() f(x)min=-
f(x)min=-![]()
∴|f(sinx)-f(cosx)|≤|f(sinx)|+|f(cosx)|≤![]()

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 时,(x-
时,(x-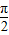 )f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )
)f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( ) 时,(x-
时,(x- )f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )
)f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( ) 时,(x-
时,(x- )f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )
)f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )