题目内容
设定义域在R上的函数f(x)是最小正周期为2π的偶函数,f′(x)是f(x)的导函数,当∈[0,π]时,0<f(x)<1;x∈(0,π)且x≠ 时,(x-
时,(x- )f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )
)f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )A.2
B.5
C.4
D.8
【答案】分析:由题意x∈(0,π) 当x∈(0,π) 且x≠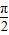 时,(x-
时,(x-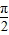 )f′(x)<0以
)f′(x)<0以 为分界点进行讨论,确定函数的单调性,利用函数的图形,画出草图进行求解,即可得到结论
为分界点进行讨论,确定函数的单调性,利用函数的图形,画出草图进行求解,即可得到结论
解答:解:∵当x∈[0,π]时,0<f(x)<1,f(x)为偶函数,
∴当x∈[-π,0]时,0<f(x)<1;
又∵f(x)的最小正周期为2π
∴当x∈[-2π,2π]时,0<f(x)<1;
∵x∈(0,π)且x≠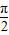 时,(x-
时,(x-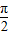 )f′(x)<0
)f′(x)<0
∴当x∈(0,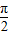 )时,f′(x)>0,f(x)单调递增;当x∈(
)时,f′(x)>0,f(x)单调递增;当x∈(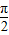 ,π)时,f′(x)<0,f(x)单调递减
,π)时,f′(x)<0,f(x)单调递减
y=f(x)与y=cosx的草图如下:
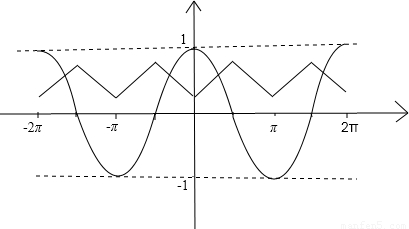
∴方程f(x)=cosx在[-2π,2π]上的又4个根
故选C
点评:本题考查函数的单调性,考查函数的零点,考查函数的周期性与奇偶性,利用数形结合的思想来求解,会化难为易
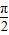 时,(x-
时,(x-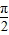 )f′(x)<0以
)f′(x)<0以 为分界点进行讨论,确定函数的单调性,利用函数的图形,画出草图进行求解,即可得到结论
为分界点进行讨论,确定函数的单调性,利用函数的图形,画出草图进行求解,即可得到结论解答:解:∵当x∈[0,π]时,0<f(x)<1,f(x)为偶函数,
∴当x∈[-π,0]时,0<f(x)<1;
又∵f(x)的最小正周期为2π
∴当x∈[-2π,2π]时,0<f(x)<1;
∵x∈(0,π)且x≠
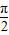 时,(x-
时,(x-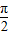 )f′(x)<0
)f′(x)<0∴当x∈(0,
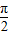 )时,f′(x)>0,f(x)单调递增;当x∈(
)时,f′(x)>0,f(x)单调递增;当x∈(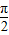 ,π)时,f′(x)<0,f(x)单调递减
,π)时,f′(x)<0,f(x)单调递减y=f(x)与y=cosx的草图如下:

∴方程f(x)=cosx在[-2π,2π]上的又4个根
故选C
点评:本题考查函数的单调性,考查函数的零点,考查函数的周期性与奇偶性,利用数形结合的思想来求解,会化难为易

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 时,(x-
时,(x-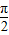 )f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )
)f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( ) 时,(x-
时,(x- )f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )
)f′(x)<0,则方程f(x)=cosx在[-2π,2π]上的根的个数( )