题目内容
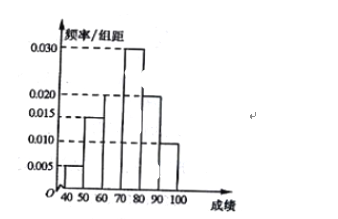
【题目】某中学举行了数学测试，并从中随机抽取了60名学生的成绩（满分100分）作为样本，其中成绩不低于80分的学生被评为优秀生，得到成绩分布的频率分布直方图如图所示.
（I）若该所中学共有3000名学生，试利用样本估计全校这次考试中优秀生人数；
（II）若在样本中，利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人，再从中抽取3人，试求恰好抽中1名优秀生的概率.
【答案】(Ⅰ)900；(Ⅱ)
.
【解析】分析：(1) 由直方图可知，样本中数据落在
的频率为
，则估计全校这次考试中优秀生人数为
；(2)利用列举法可得从这
人中抽取
人的所有可能结果有
种，其中恰好抽中
名优秀生的结果有
种，利用古典概型概率公式可得结果.
详解：（1）由直方图可知，样本中数据落在的频率为，则估计全校这次考试中优秀生人数为．
（2）由分层抽样知识可知，成绩在
，
，
间分别抽取了3人，2人，1人．
记成绩在的3人为
，
，
，成绩在的2人为
，
，成绩在的1人为
，则从这6人中抽取3人的所有可能结果有
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共20种，
其中恰好抽中1名优秀生的结果有，，
，， 
，，，
共9种，
所以恰好抽中1名优秀生的概率为
．
练习册系列答案
相关题目
