题目内容
7.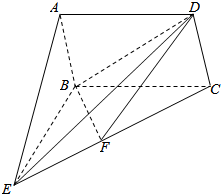 已知矩形ABCD⊥平面BCE,且EB⊥BC,点F是BC的中点,且EB=BC.
已知矩形ABCD⊥平面BCE,且EB⊥BC,点F是BC的中点,且EB=BC.(1)求证:平面BDF⊥平面ECD;
(2)求证:AE∥平面BDF;
(3)求证:平面ADE与平面BCE的交线与BC平行.
分析 (1)证明BF⊥平面ECD,即可证明平面BDF⊥平面ECD;
(2)连接AC交BD于O,连接OF,利用已知ABCD是矩形得到OF∥AE,再由线面平行的判定定理可证;
(3)证明AD∥平面BCE,利用线面平行的性质定理即可证明.
解答 证明:(1)∵矩形ABCD⊥平面BCE,DC⊥BC,
∴DC⊥平面BCE,
∵BF?平面BCE,
∴DC⊥BF,
∵点F是BC的中点,且EB=BC,
∴BF⊥CE,
∵DC∩CE=C,
∴BF⊥平面ECD,
∵BF?平面BDF,
∴平面BDF⊥平面ECD;
(2)连接AC交BD于O,连接OF,如图
在△ACE中,
∵四边形ABCD是矩形,
∴O为AC的中点,又F为EC的中点,
∴OF∥AE,又OF?平面BDF,AE?平面BDF
∴AE∥平面BDF.
(3)∵AD∥BC,AD?平面BCE,BC?平面BCE,
∴AD∥平面BCE,
设平面ADE与平面BCE的交线为l,则AD∥l,
∵AD∥BC,
∴BC∥l.
点评 本题考查了空间点线面的位置关系、线面平行和线面垂直的证明,考查了学生的空间想象能力、推理能力以及转化的数学思想.

练习册系列答案
相关题目
17.设集合A={x|2x-x2>0},B={x|x>1},R为实数集,则(∁RB)∩A等于( )
| A. | (0,1) | B. | [1,2) | C. | (0,1] | D. | (-∞,0) |
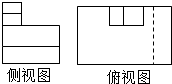
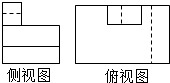
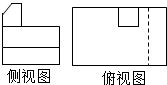
 如图所示是一位同学画的一个实物的三视图,老师判断正视图是正确的,其他两个视图有错误,则正确的侧视图和俯视图是( )
如图所示是一位同学画的一个实物的三视图,老师判断正视图是正确的,其他两个视图有错误,则正确的侧视图和俯视图是( )