题目内容
11.一个直三棱柱被一个平面截后剩余部分的三视图如图,则截去部分的体积与剩余部分的体积之比为( )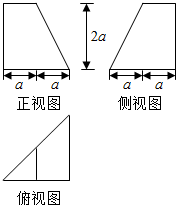
| A. | 1:2 | B. | 2:3 | C. | 4:5 | D. | 5:7 |
分析 由三视图还原原图形,作出图形,分别利用柱体、台体的体积公式运算求得答案.
解答  解:由三视图还原原几何体如图:
解:由三视图还原原几何体如图:
截去的部分为五面体BB1C1CEF,剩余的部分为三棱台ACB-A1EF,
由三视图可知,原直三棱柱底面是边长为2a的等腰直角三角形,
高为2a,
则原直三棱柱的体积为$\frac{1}{2}×2a×2a×2a=4{a}^{3}$,
三棱台的上底面的面积为$\frac{1}{2}{a}^{2}$,下底面的面积为$\frac{1}{2}×2a×2a=2{a}^{2}$,
则三棱台的体积为$\frac{1}{3}×2a(\frac{1}{2}{a}^{2}+\sqrt{\frac{1}{2}{a}^{2}×2{a}^{2}}+2{a}^{2})$=$\frac{7}{3}{a}^{3}$,
∴截去部分的体积为$4{a}^{3}-\frac{7}{3}{a}^{3}=\frac{5}{3}{a}^{3}$,
则截去部分的体积与剩余部分的体积之比为$\frac{\frac{5}{3}{a}^{3}}{\frac{7}{3}{a}^{3}}$=5:7.
故选:D.
点评 本题考查棱柱、棱锥、棱台的体积,关键是由三视图还原原图形,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.数列{an}满足a1=1,Sn=n,则a2012=( )
| A. | 1 | B. | 2010 | C. | 2011 | D. | 2012 |
1.设a,b∈R,下列不等式中恒成立的是( )
| A. | $a+\frac{1}{a}≥2$ | B. | $\frac{a}{b}+\frac{b}{a}≥2$ | C. | a2+b2>2ab | D. | $\frac{{{a^2}+3}}{{\sqrt{{a^2}+2}}}>2$ |
 已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.
已知向量$\overrightarrow{a}$=($\sqrt{2}$sinx,$\frac{{\sqrt{2}}}{2}$(cosx+sinx)),$\overrightarrow{b}$=(cosx,sinx-cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.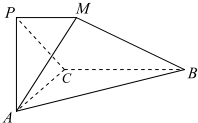 在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=4,$AB=2\sqrt{5}$.
在如图所示的多面体PMBCA中,平面PAC⊥平面ABC,△PAC是边长为2的正三角形,PM∥BC,且BC=4,$AB=2\sqrt{5}$.