题目内容
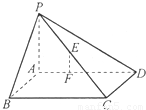
 (理)如图,四棱锥P-ABCD的底面是矩形,PA⊥面ABCD,PA=2
(理)如图,四棱锥P-ABCD的底面是矩形,PA⊥面ABCD,PA=2| 19 |
(1)求EF的长;
(2)证明:EF⊥PC.
分析:(1)以A为原点,
,
,
分别为x,y,z轴建立直角坐标系,根据已知条件求出F,P,C,E点的坐标,利用两点间距离公式即可求得EF长;
(2)由(1)求出向量
,
的坐标,只需证明
•
=0;
| AB |
| AD |
| AP |
(2)由(1)求出向量
| EF |
| PC |
| EF |
| PC |
解答: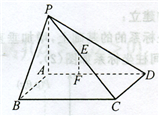 解:(1)以A为原点,
解:(1)以A为原点,
,
,
分别为x,y,z轴建立直角坐标系,
由条件知:AF=2,
∴F(0,2,0),P(0,0,2
),C(8,6,0),从而E(4,3,
),
∴EF=
=6.
(2)证明:
=(-4,-1,-
),
=(8,6,-2
),
∵
•
=-4×8+(-1)×6+(-
)×(-2
)=0,
∴EF⊥PC.
 解:(1)以A为原点,
解:(1)以A为原点,| AB |
| AD |
| AP |
由条件知:AF=2,
∴F(0,2,0),P(0,0,2
| 19 |
| 19 |
∴EF=
(4-0)2+(3-2)2+(
|
(2)证明:
| EF |
| 19 |
| PC |
| 19 |
∵
| EF |
| PC |
| 19 |
| 19 |
∴EF⊥PC.
点评:本题考查空间两点间的距离公式、直线与直线垂直的判定,考查空间向量在立体几何中的应用,考查学生的计算能力,属中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
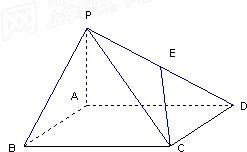 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点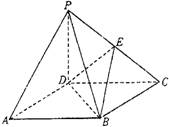

 ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.