Question

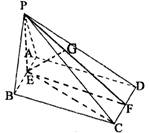
（08年惠州一中三模理） 如图，四棱锥P―ABCD的底面是AB=2，BC=的矩形，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD

   （I）证明：侧面PAB⊥侧面PBC；

   （II）求侧棱PC与底面ABCD所成的角；

 （III）求直线AB与平面PCD的距离．

 

Answer 1

解析：（I）证明：在矩形ABCD中，BC⊥AB

         又∵面PAB⊥底面ABCD侧面PAB∩底面ABCD=AB

         ∴BC⊥侧面PAB       又∵BC侧面PBC

         ∴侧面PAB⊥侧面PBC）

  （II）解：取AB中点E，连结PE、CE

         又∵△PAB是等边三角形   ∴PE⊥AB 

         又∵侧面PAB⊥底面ABCD，∴PE⊥面ABCD

         ∴∠PCE为侧棱PC与底面ABCD所成角

        

         在Rt△PEC中，∠PCE=45°为所求

   （Ⅲ）解：在矩形ABCD中，AB//CD

         ∵CD侧面PCD，AB侧面PCD，∴AB//侧面PCD

         取CD中点F，连EF、PF，则EF⊥AB

         又∵PE⊥AB    ∴AB⊥平面PEF   又∵AB//CD

         ∴CD⊥平面PEF   ∴平面PCD⊥平面PEF

         作EG⊥PF，垂足为G，则EC⊥平面PCD

         在Rt△PEF中，EG=为所求.