题目内容
(08年龙岩一中冲刺理)(12分)
如图,四棱锥P―ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明PA//平面BDE;
(2)求二面角B―DE―C的大小;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
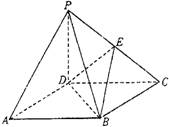
解析:解法一:(1)连结AC,设AC与BD交于O点,连结EO.
由底面ABCD是正方形知O为AC的中点,又E为PC的中点,
|
∴OE//PA, ∵OE![]() 平面BDE,
平面BDE,![]() 平面BDE,
平面BDE,
∴PA//平面BDE ………………4分
(2)∵PD⊥底面ABCD,∴PD⊥BC,又BC⊥CD,
∴BC⊥平面PCD,又PD=DC,E为PC的中点,
∴DE⊥PC,从而由三垂线定理知DE⊥BE,
∴∠BEC是二面角B―DE―C的平面角.
设正方形ABCD的边长为a,
则![]() ,
,
在Rt△BCE中,![]()
∴二面角B―DE―C的大小为![]() …………8分
…………8分
(3)作EF⊥PB于点F,则Rt△PEF∽Rt△PBC,∴![]()
∴PF?PB=PE?PC=![]() ,连结DF
,连结DF
∵在△PBD中,∠PDB=90°,PF?PB=a2=PD2, ∴PB⊥DF,
从而PB⊥平面DEF,此时![]()
即在棱PB上存在点F,![]() ,使得PB⊥平面DEF …………12分
,使得PB⊥平面DEF …………12分
解法二:(1)以D为坐标原点,分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),
B(2,2,0) ![]()
设 ![]() 是平面BDE的一个法向量,
是平面BDE的一个法向量,
则由 
∵![]() ……4分
……4分

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目

