题目内容
一农民有基本农田2亩,根据往年经验,若种水稻,则每季亩产量为400公斤;若种花生,则每季亩产量为100公斤.但水稻成本较高,每季每亩240元,而花生只需80元;且花生每公斤卖5元,稻米每公斤卖3元.现该农民手头有400元,两种作物各种多少,才能获得最大收益?
该农民种 亩水稻,
亩水稻,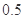 亩花生时,能获得最大利润,最大利润为1650元.
亩花生时,能获得最大利润,最大利润为1650元.
解析试题分析:解题思路:设量,列出限制条件不等式与目标函数,作可行域,平移目标函数直线,寻找最优解;求最优解,回归实际问题.规律总结:解决线性规划应用题的步骤:(1)设有关量;(2)列出线性限制条件与目标函数;(3)作可行域,平移直线找最优解;(4)求最优解:(5)作答.
试题解析:设该农民种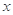 亩水稻,
亩水稻,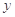 亩花生时,能获得利润
亩花生时,能获得利润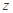 元.则
元.则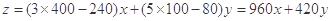 即
即
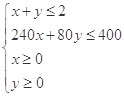 即
即 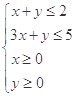
作出可行域如图阴影部分所示, 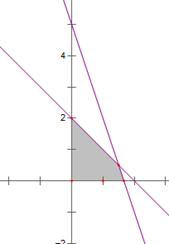
作出基准直线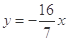 ,在可行域内平移直线
,在可行域内平移直线 ,可知当直线过点
,可知当直线过点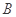 时,纵截距
时,纵截距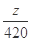 有最大值,
有最大值,
由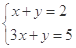 解得
解得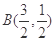 ,
,
故当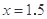 ,
,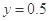 时,
时,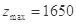 元,
元,
答:该农民种 亩水稻,
亩水稻,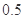 亩花生时,能获得最大利润,最大利润为1650元.
亩花生时,能获得最大利润,最大利润为1650元.
考点:线性规划.

练习册系列答案
相关题目
设函数 ,其中
,其中 ,若不等式
,若不等式 的解集为
的解集为 ,则a的值为( )
,则a的值为( )
| A.1 | B.2 | C.3 | D.4 |
 满足约束条件
满足约束条件 ,目标函数
,目标函数 的最小值是 。
的最小值是 。
 中,已知点
中,已知点 ,点
,点 在
在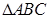 三边围成的区域(含边界)上,且
三边围成的区域(含边界)上,且 .
. ,求
,求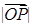 ;
; 表示
表示 ,并求
,并求 表示的区域为
表示的区域为 ,不等式
,不等式 表示的平面区域为
表示的平面区域为 .
. =;
=; 为
为 万元投资甲项目,
万元投资甲项目, 万元投资乙项目,试写出
万元投资乙项目,试写出
 、
、 满足约束条件:
满足约束条件: ,则
,则 的最小值是
的最小值是  x3+
x3+ ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在的区域面积S.
ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),求动点(a,b)所在的区域面积S.