题目内容
设函数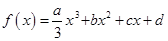 (其中
(其中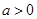 ),且方程
),且方程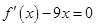 的两个根分别为
的两个根分别为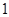 、
、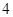 .
.
(1)当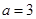 且曲线
且曲线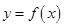 过原点时,求
过原点时,求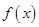 的解析式;
的解析式;
(2)若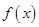 在
在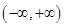 无极值点,求
无极值点,求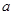 的取值范围.
的取值范围.
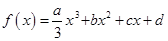 (其中
(其中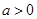 ),且方程
),且方程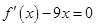 的两个根分别为
的两个根分别为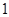 、
、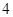 .
.(1)当
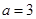 且曲线
且曲线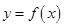 过原点时,求
过原点时,求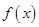 的解析式;
的解析式;(2)若
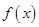 在
在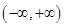 无极值点,求
无极值点,求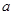 的取值范围.
的取值范围.(1)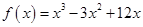 ;(2)实数
;(2)实数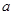 的取值范围是
的取值范围是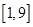 .
.
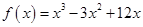 ;(2)实数
;(2)实数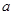 的取值范围是
的取值范围是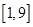 .
.试题分析:(1)先将
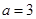 代入函数
代入函数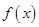 的解析式,利用“曲线
的解析式,利用“曲线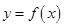 过原点”先求出
过原点”先求出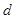 的值,然后求出二次函数
的值,然后求出二次函数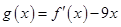 的解析式,利用“
的解析式,利用“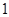 、
、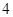 为二次方程
为二次方程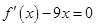 的两个根”并结合韦达定理求出
的两个根”并结合韦达定理求出 、
、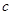 的值,最终确定函数
的值,最终确定函数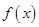 的解析式;(2)先利用“
的解析式;(2)先利用“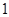 、
、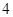 为二次方程
为二次方程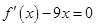 的两个根”并结合韦达定理确定
的两个根”并结合韦达定理确定 、
、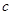 与
与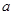 的关系,然后求出
的关系,然后求出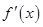 ,对
,对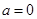 与
与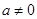 进行分类讨论,将
进行分类讨论,将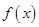 在
在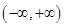 无极值点进行转化,对
无极值点进行转化,对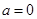 进行检验;当
进行检验;当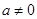 时,得到
时,得到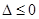 ,从而求出实数
,从而求出实数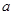 的取值范围.
的取值范围.试题解析:(1)当
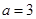 时,
时, ,
,由于曲线
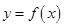 过原点,则有
过原点,则有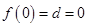 ,
,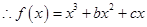 ,
,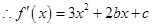 ,令
,令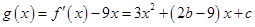 ,
,由题意知,
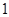 、
、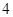 是二次函数
是二次函数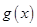 的两个零点,由韦达定理得
的两个零点,由韦达定理得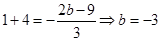 ,
,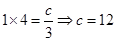 ,
,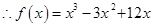 ;
;(2)
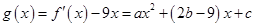 ,
,由于
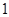 、
、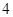 是二次函数
是二次函数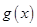 的两个零点,由韦达定理得
的两个零点,由韦达定理得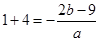 ,
,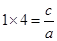 ,
,解得
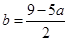 ,
,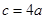 ,
,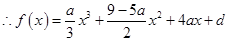 ,
,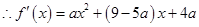 ,
,当
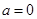 时,
时, ,令
,令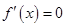 ,解得
,解得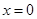 ,当
,当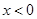 时,
时,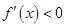 ,当
,当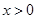 ,
,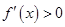 ,
,此时
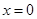 为函数
为函数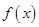 的极小值点,不合乎题意;
的极小值点,不合乎题意;故
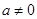 ,由于函数
,由于函数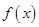 在
在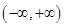 无极值点,则
无极值点,则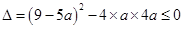 ,
,即
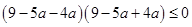 ,化简得
,化简得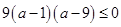 ,解得
,解得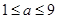 ,
,故实数
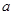 的取值范围是
的取值范围是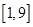 .
.
练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 ,其中
,其中 ,
, ,
, 为
为 上的减函数,求
上的减函数,求 应满足的关系;
应满足的关系;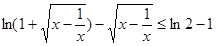 。
。 ,函数
,函数 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 无零点,求实数
无零点,求实数 的取值范围;
的取值范围; 、
、 ,求证:
,求证: .
.
 时,求函数
时,求函数 的最大值;
的最大值; (
( )其图象上任意一点
)其图象上任意一点 处切线的斜率
处切线的斜率 ≤
≤ 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.
 试确定函数
试确定函数 的单调区间;
的单调区间; ,且对于任意
,且对于任意 ,
, 恒成立,求实数
恒成立,求实数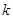 的取值范围;
的取值范围; 若至少存在一个实数
若至少存在一个实数 ,使
,使 成立,求实数
成立,求实数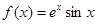 .
.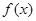 的单调区间;
的单调区间;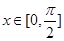 ,
,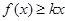 总成立,求实数
总成立,求实数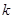 的取值范围;
的取值范围;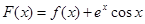 ,
,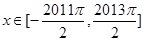 ,过点
,过点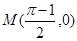 作函数
作函数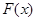 图象的所有切线,令各切点得横坐标构成数列
图象的所有切线,令各切点得横坐标构成数列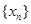 ,求数列
,求数列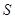 的值.
的值.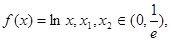 且
且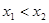 则下列结论正确的是( )
则下列结论正确的是( )



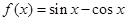 且
且 是f(x)的导函数,若
是f(x)的导函数,若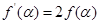 ,,则
,,则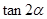 = .
= . 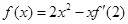 ,则函数
,则函数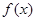 的图象在点
的图象在点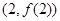 处的切线方程是 .
处的切线方程是 .