题目内容
如图放置的边长为1的正方形 沿
沿 轴正方向滚动.设顶点
轴正方向滚动.设顶点 的轨迹方程是
的轨迹方程是 ,设
,设 在其两个相邻零点间的图象与
在其两个相邻零点间的图象与 轴所围区域为S,则直线
轴所围区域为S,则直线 从
从 所匀速移动扫过区域S的面积D与
所匀速移动扫过区域S的面积D与 的函数图象大致为( ).
的函数图象大致为( ).
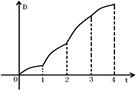



A. B. C. D.
D
解析试题分析:不难想象,从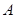 点在
点在 轴上的时候开始计算,到下一次
轴上的时候开始计算,到下一次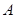 点落在
点落在 轴上,这个过程中四个顶点依次落在了
轴上,这个过程中四个顶点依次落在了 轴上,而每两个顶点间距离为正方形的边长1,下面考察
轴上,而每两个顶点间距离为正方形的边长1,下面考察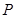 点的运动轨迹,
点的运动轨迹,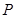 点从
点从 轴上开始运动的时候,首先是围绕
轴上开始运动的时候,首先是围绕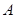 点运动
点运动 个圆,该圆半径为1,然后以
个圆,该圆半径为1,然后以 点为中心,滚动到
点为中心,滚动到 点落地,其间是以
点落地,其间是以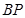 为半径,旋转90°,然后以
为半径,旋转90°,然后以 为圆心,再旋转90°,这时候以
为圆心,再旋转90°,这时候以 为半径,因此最终构成图象如下:
为半径,因此最终构成图象如下: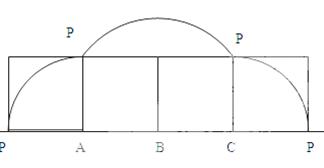
因此不难直线 从
从 所匀速移动扫过区域S的面积D与
所匀速移动扫过区域S的面积D与 的函数图象在
的函数图象在 增加速度越来越快,在
增加速度越来越快,在 上增加速度越来越慢,故选D.
上增加速度越来越慢,故选D.
考点:轨迹问题,函数图像.

练习册系列答案
相关题目
已知函数 ,则
,则 的单调递减区间为( )
的单调递减区间为( )
| A.[0,1) | B.(-∞,0) |
C. | D.(-∞,1)和(1,+∞) |
x为实数,[x]表示不超过x的最大整数,则函数f(x)=x-[x]在R上为( )
| A.奇函数 | B.偶函数 |
| C.增函数 | D.周期函数 |
已知函数f(x)= 则函数f(x)的零点为 ( ).
则函数f(x)的零点为 ( ).
A. ,0 ,0 | B.-2,0 | C. | D.0 |
已知定义在R上的函数y=f(x)满足以下三个条件:①对于任意的x∈R,都有f(x+4)=f(x);②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);③函数y=f(x+2)的图象关于y轴对称.则下列结论中正确的是( ).
| A.f(4.5)<f(7)<f(6.5) | B.f(7)<f(4.5)<f(6.5) |
| C.f(7)<f(6.5)<f(4.5) | D.f(4.5)<f(6.5)<f(7) |
定义在R上的函数f(x)的导函数为f′(x),已知f(x+1)是偶函数,且(x-1)f′(x)<0.若x1<x2,且x1+x2>2,则f(x1)与f(x2)的大小关系是( ).
| A.f(x1)<f(x2) | B.f(x1)=f(x2) |
| C.f(x1)>f(x2) | D.不确定 |
 的图象大致是( )
的图象大致是( )
 =( ).
=( ).
