题目内容
已知双曲线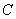 :
: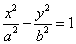
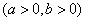 的右焦点是
的右焦点是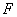 ,右顶点是
,右顶点是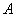 ,虚轴的上端点是
,虚轴的上端点是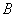 ,且
,且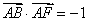 ,
,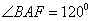 .
.
(1)求双曲线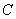 的方程;
的方程;
(2)过点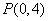 的直线
的直线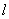 交双曲线于
交双曲线于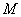 、
、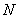 两点,交
两点,交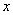 轴于点
轴于点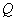 (点
(点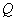 与双曲线
与双曲线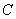 的顶点不重合).当
的顶点不重合).当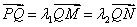 ,且
,且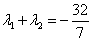 时,求点
时,求点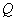 的坐标.
的坐标.
【答案】
解:(1)由条件知 ,
,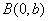 ,
,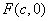 。
。
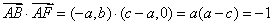 ①
①
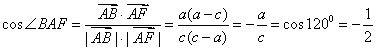
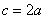 ②
②
解 ①② 得  ,
,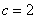 。则
。则 ,
,
故双曲线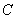 的方程为
的方程为 。
……………………
。
……………………  分
分
(2)由题意知直线 的斜率
的斜率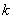 存在且不等于零。
存在且不等于零。
设 的方程为:
的方程为: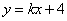 ,
,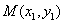 ,
, ,则
,则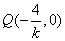 .
.
∵  , ∴
, ∴ 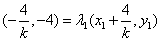
∴ 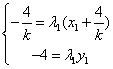
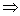
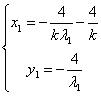 。 ……………………
。 ……………………  分
分
∵ 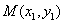 在双曲线
在双曲线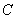 上, ∴
上, ∴ 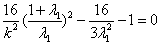 ,
,
∴ 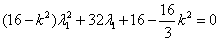 。
。
同理  。 ……………………
。 …………………… 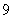 分
分
若 ,则直线
,则直线 过顶点,不合题意, ∴
过顶点,不合题意, ∴
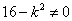 。………
。……… 分
分
∴ 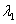 、
、 是二次方程
是二次方程  的两根。
的两根。
∴ 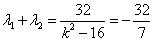 ,
,
∴ 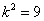 ,此时
,此时 , ∴
, ∴ .
.
∴ 所求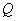 点的坐标为
点的坐标为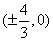 .
……………………
.
……………………  分
分

练习册系列答案
相关题目
 的左、右焦 点分别为F1、F2,P为C的右支上一点,且
的左、右焦 点分别为F1、F2,P为C的右支上一点,且 的面积等于 .
的面积等于 . 的左、右焦 点分别为F1、F2,P为C的右支上一点,且
的左、右焦 点分别为F1、F2,P为C的右支上一点,且 的面积等于 .
的面积等于 .