题目内容
判断函数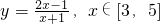 的单调性,并用函数单调性定义证明之,再求其最值.
的单调性,并用函数单调性定义证明之,再求其最值.
解:设x1,x2∈[3,5]且x1<x2
∴

∴函数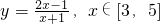 是增函数
是增函数
∴当x=5时函数取最大值为 ,当x=3时函数取得最小值为
,当x=3时函数取得最小值为 .
.
分析:在区间上任取两个变量,且界定大小,再作差变形与零比较即可,要注意变形要到位.
点评:本题主要考查函数单调性的判断与证明,以及应用单调性求函数的最值,同时还考查了学生的变形,转化能力,属中档题.
∴


∴函数
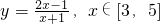 是增函数
是增函数∴当x=5时函数取最大值为
 ,当x=3时函数取得最小值为
,当x=3时函数取得最小值为 .
.分析:在区间上任取两个变量,且界定大小,再作差变形与零比较即可,要注意变形要到位.
点评:本题主要考查函数单调性的判断与证明,以及应用单调性求函数的最值,同时还考查了学生的变形,转化能力,属中档题.

练习册系列答案
相关题目