题目内容
【题目】已知函数![]() 的图象与过原点的直线恰有四个交点,设四个交点中横坐标最大值为
的图象与过原点的直线恰有四个交点,设四个交点中横坐标最大值为![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C. 0 D. 2
C. 0 D. 2
【答案】A
【解析】分析:依题意,过原点的直线与函数y=|cosx|(x≥0)在区间(![]() ,2π)内的图象相切,利用导数知识可求得切线方程,利用直线过原点,可求得θ=-
,2π)内的图象相切,利用导数知识可求得切线方程,利用直线过原点,可求得θ=-![]() ,代入所求关系式即可求得答案.
,代入所求关系式即可求得答案.
详解::∵函数f(x)=|cosx|(x≥0)的图象与过原点的直线恰有四个交点,∴直线与函数y=|cosx|(x≥0)在区间(![]() ,2π)内的图象相切,在区间(
,2π)内的图象相切,在区间(![]() ,2π)上,y的解析式为y=cosx,故由题意切点坐标为(θ,cosθ),∴切线斜率k=y′=-sinx|x=θ=-sinθ,∴由点斜式得切线方程为:y-cosθ=-sinθ(x-θ),即 y=-sinθx+θsinθ+cosθ,∵直线过原点,∴θsinθ+cosθ=0,得θ=-
,2π)上,y的解析式为y=cosx,故由题意切点坐标为(θ,cosθ),∴切线斜率k=y′=-sinx|x=θ=-sinθ,∴由点斜式得切线方程为:y-cosθ=-sinθ(x-θ),即 y=-sinθx+θsinθ+cosθ,∵直线过原点,∴θsinθ+cosθ=0,得θ=-![]() ,
,
![]()

【题目】利用独立性检验的方法调查高中生的写作水平与离好阅读是否有关,随机询问120名高中生是否喜好阅读,利用2×2列联表,由计算可得K2=4.236
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参照附表,可得正确的结论是( )
A.有95%的把握认为“写作水平与喜好阅读有关”
B.有97.5%的把握认为“写作水平与喜好阅读有关”
C.有95%的把握认为“写作水平与喜好阅读无关”
D.有97.5%的把握认为“写作水平与喜好阅读无关”
【题目】为了解人们对“![]() 年
年![]() 月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在
月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在![]() 岁到
岁到![]() 岁的人群中随机调查了
岁的人群中随机调查了![]() 人,并得到如图所示的年龄频率分布直方图,在这
人,并得到如图所示的年龄频率分布直方图,在这![]() 人中关注度非常髙的人数与年龄的统计结果如表所示:
人中关注度非常髙的人数与年龄的统计结果如表所示:
年龄 | 关注度非常高的人数 |
|
|
|
|
|
|
|
|
|
|
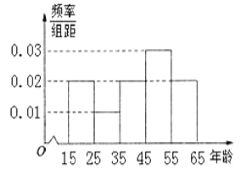
(1)由频率分布直方图,估计这![]() 人年龄的中位数和平均数;
人年龄的中位数和平均数;
(2)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以
的前提下,认为以![]() 岁为分界点的不同人群对“两会”的关注度存在差异?
岁为分界点的不同人群对“两会”的关注度存在差异?
(3)按照分层抽样的方法从年龄在![]() 岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在
岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在![]() 岁以下的概率是多少.
岁以下的概率是多少.
|
| 总计 | |
非常高 | |||
一般 | |||
总计 |
参考数据:
|
|
|
|
|
|
|
|
|
|