题目内容
乘积(a+b+c)(m+n)(x+y)展开后,共有( )
分析:根据题意,分析可得所给乘积式的结果,需要在每一个括号中选一个进行乘法运算,分别分析每个括号中的取法数目,相乘得到结果.
解答:解:根据题意,乘积(a+b+c)(m+n)(x+y)展开后的每一项是在(a+b+c)、(m+n)、(x+y)这3个式子中任取一项后相乘,
而(a+b+c)中有3种取法,(m+n)中有2种取法,(x+y)中有2种取法,
由乘法原理,可得共有3×2×2=12种取法,
即乘积(a+b+c)(m+n)(x+y)展开后,共有12项;
故选D.
而(a+b+c)中有3种取法,(m+n)中有2种取法,(x+y)中有2种取法,
由乘法原理,可得共有3×2×2=12种取法,
即乘积(a+b+c)(m+n)(x+y)展开后,共有12项;
故选D.
点评:此题主要考查乘法计数原理在求多项式乘法因式个数中的应用.对于此题分析出完成事件所需要分三步是解题的关键,题目计算量小,属于基础题目.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 为虚数单位,则
为虚数单位,则 的实部与虚部的乘积等于( )
的实部与虚部的乘积等于( )  B.
B.
 C.
C.
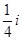 D.
D.

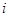 为虚数单位,则
为虚数单位,则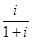 的实部与虚部的乘积等于( )
的实部与虚部的乘积等于( ) 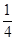 B.
B.
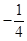 C.
C.
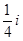 D.
D.
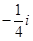
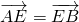 ,
,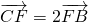 ,连接CE、DF相交于点M,若
,连接CE、DF相交于点M,若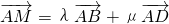 ,则实数λ与μ的乘积为
,则实数λ与μ的乘积为


