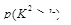题目内容
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
(Ⅰ)根据上表完成下面的2×2列联表:
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | 12 | ||
| 合计 | 20 |
(Ⅲ)若按下面的方法从这20人中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,试求:抽到12号的概率的概率.
参考数据公式:①独立性检验临界值表
| P(K2≥x0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(II)我们可以根据列联表中的数据,代入公式K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(III)本小题考查的知识点是古典概型,关键是要找出抽到12号的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
| 20×(5×12-1×2)2 |
| 6×14×7×13 |
所以我们有99.5%的把握认为:学生的数学成绩与物理成绩之间有关系.
(Ⅲ)抽到12号有4种(2,6),(4,6),(3,4),(4,3)
基本事件有36种(1,1)(1,2),(1,3),(1,4),(1,5)(1,6)
(2,1)(2,2),(2,3),(2,4),(2,5)(2,6)
(3,1)(3,2),(3,3),(3,4),(3,5)(3,6)
(4,1)(4,2),(4,3),(4,4),(4,5)(4,6)
(5,1)(5,2),(5,3),(5,4),(5,5)(5,6)
(6,1)(6,2),(6,3),(6,4),(6,5)(6,6)
所以,抽到12号的概率P=
| 4 |
| 36 |
| 1 |
| 9 |

 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
|
物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 |
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
|
|
数学成绩优秀 |
数学成绩不优秀 |
合 计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
|
|
|
合 计 |
|
|
20 |
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?
参考数据:
假设有两个分类变量 和
和 ,它们的值域分别为
,它们的值域分别为 和
和 ,其样本频数列联表(称为
,其样本频数列联表(称为 列联表)为:
列联表)为:
|
|
|
|
合计 |
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
|
则随机变量 ,其中
,其中 为样本容量;
为样本容量;
②独立检验随机变量 的临界值参考表:
的临界值参考表:
|
|
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩,列出如下所示2×2列联表:
|
数学成绩 物理成绩 |
优秀 |
不优秀 |
合计 |
|
优秀 |
5 |
2 |
7 |
|
不优秀 |
1 |
12 |
13 |
|
合计 |
6 |
14 |
20 |
(1)根据题中表格的数据计算,你有多少的把握认为学生的数学成绩与物理成绩之间有关系?
(2)若按下面的方法从这20人(序号1,2,3,…,20)中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:①抽到12号的概率;②抽到 “无效序号(序号大于20)”的概率.
参考公式: ,其中
,其中 )
)
临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取
高二年级20名学生某次考试成绩,列出如下所示2×2列联表:
|
数学成绩 物理成绩 |
优秀 |
不优秀 |
合计 |
|
优秀 |
5 |
2 |
7 |
|
不优秀 |
1 |
12 |
13 |
|
合计 |
6 |
14 |
20 |
(1)根据题中表格的数据计算,你有多少的把握认为学生的数学成绩与物理成绩之间有关系?
(2)若按下面的方法从这20人(序号1,2,3,…,20)中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:①抽到12号的概率;②抽到“无效序号(序号大于20)”的概率.
参考公式: ,其中
,其中 )
)
临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |