题目内容
设F是椭圆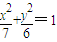 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为 .
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为 .
【答案】分析:若这个等差数列是增数列,则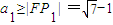 ,
,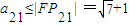 ;若这个等差数列是减数列,则
;若这个等差数列是减数列,则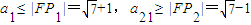 ,由此可求出d的取值范围.
,由此可求出d的取值范围.
解答:解:若这个等差数列是增数列,则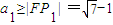 ,
,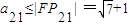 ,
,
∴a21=a1+20d,∴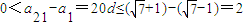 ,
,
解得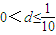 .
.
若这个等差数列是减数列,则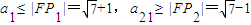 ,
,
∴a21=a1+20d,∴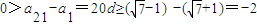 ,
,
解得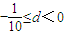 .
.
∴d的取值范围为 .
.
答案: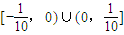 .
.
点评:本题以椭圆知识为载体考查数列知识,体现了出题人的智慧.
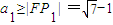 ,
,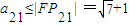 ;若这个等差数列是减数列,则
;若这个等差数列是减数列,则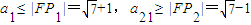 ,由此可求出d的取值范围.
,由此可求出d的取值范围.解答:解:若这个等差数列是增数列,则
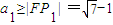 ,
,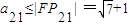 ,
,∴a21=a1+20d,∴
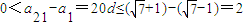 ,
,解得
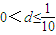 .
.若这个等差数列是减数列,则
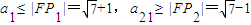 ,
,∴a21=a1+20d,∴
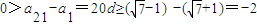 ,
,解得
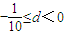 .
.∴d的取值范围为
 .
.答案:
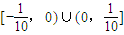 .
.点评:本题以椭圆知识为载体考查数列知识,体现了出题人的智慧.

练习册系列答案
相关题目
 (2012•河北模拟)如图,已知椭圆
(2012•河北模拟)如图,已知椭圆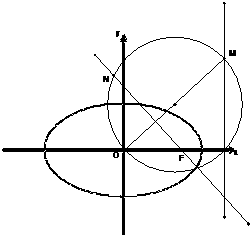 (2011•石景山区一模)已知椭圆
(2011•石景山区一模)已知椭圆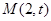
 在直线
在直线 上。
上。 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程; 经过点
经过点 ,离心率为
,离心率为 ,动点
,动点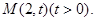
 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;