题目内容
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
【答案】分析:先设出相应的坐标,然后用要求的点的坐标表示出已知轨迹方程的图象上的点的坐标,再代入已知的轨迹方程,即可求出点P的横纵坐标的方程.本题宜先借且图象分析其几何 特征,将几何特征进行正确转化.
解答:解:设动点P(x,y),由题意可知P是△ABD的重心,故连接AD.
由A(-1,0),B(1,0),令动点C(x,y),则D(2x-1,2y),
由重心坐标公式: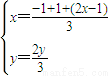 则
则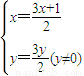
代入x2+y2=1,整理得所求轨迹方程为(x+ )2+y2=
)2+y2= (y≠0).
(y≠0).
点评:考查代入法求轨迹方程,本题对识图的能力要求较高.尤其是P点是三角形的重心这个结论的发现,必对图形进行细致的分析事才能发现.
解答:解:设动点P(x,y),由题意可知P是△ABD的重心,故连接AD.
由A(-1,0),B(1,0),令动点C(x,y),则D(2x-1,2y),
由重心坐标公式:
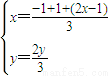 则
则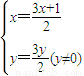
代入x2+y2=1,整理得所求轨迹方程为(x+
 )2+y2=
)2+y2= (y≠0).
(y≠0).点评:考查代入法求轨迹方程,本题对识图的能力要求较高.尤其是P点是三角形的重心这个结论的发现,必对图形进行细致的分析事才能发现.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
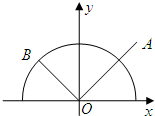 如图,已知点A(1,1)和单位圆上半部分上的动点B.
如图,已知点A(1,1)和单位圆上半部分上的动点B. 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程. 如图,已知点A(1,1)和单位圆上半部分上的动点B.
如图,已知点A(1,1)和单位圆上半部分上的动点B. ,求向量
,求向量 ;
;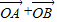 |的最大值.
|的最大值. 如图,已知点A(1,1)和单位圆上半部分上的动点B.
如图,已知点A(1,1)和单位圆上半部分上的动点B.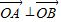 ,求向量
,求向量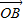 ;
; |的最大值.
|的最大值.