题目内容
 如图,已知点A(1,1)和单位圆上半部分上的动点B.
如图,已知点A(1,1)和单位圆上半部分上的动点B.(1)若
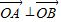 ,求向量
,求向量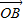 ;
;(2)求|
 |的最大值.
|的最大值.
【答案】分析:(1)根据题意设出B(cosθ,sinθ),0≤θ≤π,在根据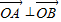 列出关于θ的三角方程即可
列出关于θ的三角方程即可
(2)根据|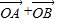 |的定义将之转化为关于θ的三角函数
|的定义将之转化为关于θ的三角函数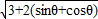 ,并将之平方得
,并将之平方得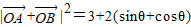 ,最后在将sinθ+cosθ平方求出范围即可
,最后在将sinθ+cosθ平方求出范围即可
解答:解:(1)依题意,B(cosθ,sinθ),0≤θ≤π(不含1个或2个端点也对)
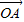 =(1,1),
=(1,1),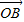 =(cosθ,sinθ)(写出1个即可),
=(cosθ,sinθ)(写出1个即可),
因为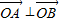 ,所以
,所以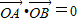 ,即cosθ+sinθ=0,
,即cosθ+sinθ=0,
解得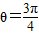 ,所以OB=(-
,所以OB=(-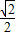 ,
,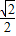 ).
).
(2)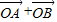 =(1+cosθ,1+sinθ),
=(1+cosθ,1+sinθ),
则|OA+OB|=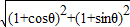 =
=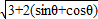 ,
,
∴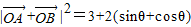 ,
,
令t=sinθ+cosθ,则t2=1+sin2θ≤2,即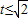 ,
,
∴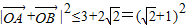 ,有
,有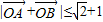
当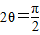 ,即
,即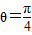 时,|
时,|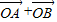 |取得最大值
|取得最大值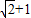 .
.
点评:本题考查了向量在几何中的应用,解三角方程以及三角函数知识,属于基础题.
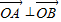 列出关于θ的三角方程即可
列出关于θ的三角方程即可(2)根据|
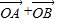 |的定义将之转化为关于θ的三角函数
|的定义将之转化为关于θ的三角函数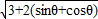 ,并将之平方得
,并将之平方得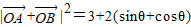 ,最后在将sinθ+cosθ平方求出范围即可
,最后在将sinθ+cosθ平方求出范围即可解答:解:(1)依题意,B(cosθ,sinθ),0≤θ≤π(不含1个或2个端点也对)
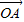 =(1,1),
=(1,1),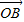 =(cosθ,sinθ)(写出1个即可),
=(cosθ,sinθ)(写出1个即可),因为
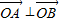 ,所以
,所以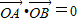 ,即cosθ+sinθ=0,
,即cosθ+sinθ=0,解得
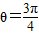 ,所以OB=(-
,所以OB=(-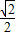 ,
,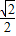 ).
).(2)
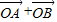 =(1+cosθ,1+sinθ),
=(1+cosθ,1+sinθ),则|OA+OB|=
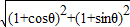 =
=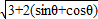 ,
,∴
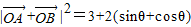 ,
,令t=sinθ+cosθ,则t2=1+sin2θ≤2,即
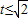 ,
,∴
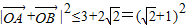 ,有
,有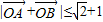
当
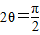 ,即
,即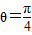 时,|
时,|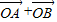 |取得最大值
|取得最大值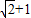 .
.点评:本题考查了向量在几何中的应用,解三角方程以及三角函数知识,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
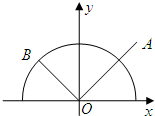 如图,已知点A(1,1)和单位圆上半部分上的动点B.
如图,已知点A(1,1)和单位圆上半部分上的动点B. 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程. 如图,已知点A(1,1)和单位圆上半部分上的动点B.
如图,已知点A(1,1)和单位圆上半部分上的动点B. ,求向量
,求向量 ;
;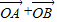 |的最大值.
|的最大值.