题目内容
(本小题共14分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点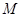 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
).
【答案】
(Ⅰ)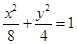 .
.
(Ⅱ)直线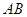 过定点(
过定点(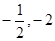 ).
).
【解析】本试题主要是考查了椭圆的方程的求解以及直线与椭圆的位置关系的运用。
(1)利用椭圆的性质得到关于系数a,b,c的关系式,然后求解得到椭圆的方程。
(2)对于直线斜率是否存在进行分类讨论,然后设出直线与椭圆联立方程组,借助于韦达定理和斜率的关系式得到直线恒过定点。
解:(Ⅰ)由已知可得 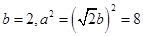 ,
,
所求椭圆方程为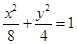 .
………5分
.
………5分
(Ⅱ)若直线 的斜率存在,设
的斜率存在,设 方程为
方程为 ,依题意
,依题意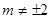 .
.
设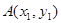 ,
,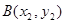 ,
,
由 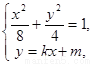 得
得 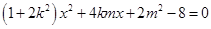 .
.
则 .
………8分
.
………8分
由已知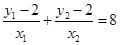 ,所以
,所以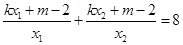 ,
,
即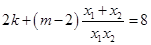 .
………10分
.
………10分
所以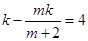 ,整理得
,整理得  .
.
故直线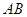 的方程为
的方程为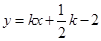 ,即
,即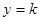 (
(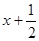 )
)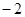 .
.
所以直线 过定点(
过定点(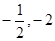 ).
………12分
).
………12分
若直线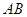 的斜率不存在,设
的斜率不存在,设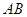 方程为
方程为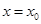 ,
,
设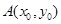 ,
,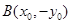 , 由已知
, 由已知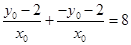 ,
,
得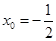 .此时
.此时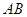 方程为
方程为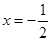 ,显然过点(
,显然过点(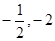 ).
).
综上,直线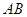 过定点(
过定点(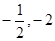 ).
………14分
).
………14分

练习册系列答案
相关题目
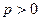 ,动点
,动点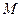 到定点
到定点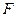
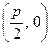 的距离比
的距离比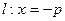 的距离小
的距离小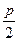 .
.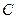 的方程;
的方程; 是轨迹
是轨迹 的两个不同点,
的两个不同点,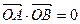 ,求
,求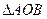 面积的最小值;
面积的最小值;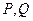 关于直线
关于直线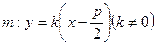 对称?若存在,求出直线
对称?若存在,求出直线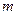 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.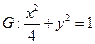 .过点(m,0)作圆
.过点(m,0)作圆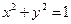 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.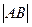 表示为m的函数,并求
表示为m的函数,并求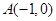 ,
,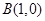 ,动点P满足
,动点P满足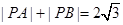 ,记动点P的轨迹为W.
,记动点P的轨迹为W.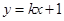 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点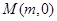 ,使得
,使得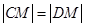 成立,求实数m的取值范围.
成立,求实数m的取值范围.