题目内容
(08年北京卷文)(本小题共14分)
已知![]() 的顶点
的顶点![]() 在椭圆
在椭圆![]() 上,
上,![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(Ⅰ)当![]() 边通过坐标原点
边通过坐标原点![]() 时,求
时,求![]() 的长及
的长及![]() 的面积;
的面积;
(Ⅱ)当![]() ,且斜边
,且斜边![]() 的长最大时,求
的长最大时,求![]() 所在直线的方程.
所在直线的方程.
解:(Ⅰ)因为![]() ,且
,且![]() 边通过点
边通过点![]() ,所以
,所以![]() 所在直线的方程为
所在直线的方程为![]() .
.
设![]() 两点坐标分别为
两点坐标分别为![]() .
.
由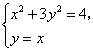 得
得![]() .
.
所以![]() .
.
又因为![]() 边上的高
边上的高![]() 等于原点到直线
等于原点到直线![]() 的距离.
的距离.
所以![]() ,
,![]() .
.
(Ⅱ)设![]() 所在直线的方程为
所在直线的方程为![]() ,
,
由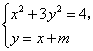 得
得![]() .
.
因为![]() 在椭圆上,
在椭圆上,
所以![]() .
.
设![]() 两点坐标分别为
两点坐标分别为![]() ,
,
则![]() ,
,![]() ,
,
所以![]() .
.
又因为![]() 的长等于点
的长等于点![]() 到直线
到直线![]() 的距离,即
的距离,即![]() .
.
所以![]() .
.
所以当![]() 时,
时,![]() 边最长,(这时
边最长,(这时![]() )
)
此时![]() 所在直线的方程为
所在直线的方程为![]() .
.
【高考考点】直线与圆锥曲线的位置关系
【易错提醒】解析几何的综合题在高考中的“综合程度”往往比较高,且计算量常常较大,因此平时复习时要注意其深难度,同时注意加强计算能力的培养

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目