题目内容
四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为
的等腰三角形,则二面角V-AB-C的大小为( )
| 5 |
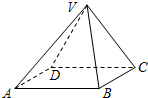
分析:由题意可知:四棱锥V-ABCD是正四棱锥,连接AC,BD,相交于点O,连接VO,则VO⊥平面ABCD.取AB的中点M,连接VM,OM.则AB⊥OM,利用三垂线定理可得AB⊥VM.
即可得到∠OMV是二面角V-AB-C的平面角.在Rt△VOM,利用边角关系即可得出.
即可得到∠OMV是二面角V-AB-C的平面角.在Rt△VOM,利用边角关系即可得出.
解答:解:如图所示,
由题意可得:四棱锥V-ABCD是正四棱锥,连接AC,BD,相交于点O,连接VO,则VO⊥平面ABCD.
取AB的中点M,连接VM,OM.则AB⊥OM,∴AB⊥VM.
∴∠OMV是二面角V-AB-C的平面角.
由正方形可得:OB=
BD=
×2
=
.
∴VO=
=
=
.
在Rt△VOM,tan∠VMO=
=
=
.
∴∠VMO=60°.
故选C.

由题意可得:四棱锥V-ABCD是正四棱锥,连接AC,BD,相交于点O,连接VO,则VO⊥平面ABCD.
取AB的中点M,连接VM,OM.则AB⊥OM,∴AB⊥VM.
∴∠OMV是二面角V-AB-C的平面角.
由正方形可得:OB=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴VO=
| VB2-OB2 |
(
|
| 3 |
在Rt△VOM,tan∠VMO=
| VO |
| OM |
| ||
| 1 |
| 3 |
∴∠VMO=60°.
故选C.
点评:熟练掌握正四棱锥的性质、正方形的性质、二面角的平面角的作法、直角三角形的边角关系等是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
在底面为平行四边形的四棱锥V-ABCD中,
=2
,则三棱锥E-BCD与五面体VABED的体积之比为( )
| VE |
| EC |
| A、1:3 | B、1:4 |
| C、1:5 | D、1:6 |
 四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为
四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD. (2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ASCD.设AB=2.
(2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ASCD.设AB=2.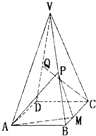 (2013•乌鲁木齐一模)在正四棱锥V-ABCD中,P,Q分别为棱VB,VD的中点,点 M 在边 BC 上,且 BM:BC=1:3,AB=2
(2013•乌鲁木齐一模)在正四棱锥V-ABCD中,P,Q分别为棱VB,VD的中点,点 M 在边 BC 上,且 BM:BC=1:3,AB=2