题目内容
 (2007•深圳一模)请从下面两题中选做一题,如果两题都做,以第一题的得分为最后得分.
(2007•深圳一模)请从下面两题中选做一题,如果两题都做,以第一题的得分为最后得分.(1)在极坐标系中,过圆ρ=4cosθ的圆心,且垂直于极轴的直线方程为
ρcosθ=2
ρcosθ=2
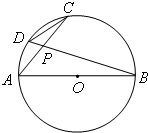
.(2)如图,AB为⊙O的直径,弦AC、BD交于点P,若AB=3,CD=1,则sin∠APD=
2
| ||
| 3 |
2
| ||
| 3 |
分析:(1)先将原极坐标方程ρ=4cosθ的两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行求解即可.
(2)由圆周角定理,我们可得∠A=∠D,∠B=∠C,结合相似三角形判断定理可得△ABP∽△DCP,进而由相似三角形的性质我们可得DP:AP=DC:AB=
,即cos∠APD=
,再由同角三角函数关系,即可得到答案.
(2)由圆周角定理,我们可得∠A=∠D,∠B=∠C,结合相似三角形判断定理可得△ABP∽△DCP,进而由相似三角形的性质我们可得DP:AP=DC:AB=
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:(1)由题意可知圆的标准方程为(x-3)2+y2=4,圆心是(2,0),
所求直线标准方程为x=2,
则极坐标方程为ρcosθ=2.
故答案为:ρcosθ=2.
(2)解:由圆周角定理,可得:
在△ABP和△DCP中
∠A=∠D,∠B=∠C
∴△ABP∽△DCP
所以DP:AP=DC:AB=
连接DA
因为AB是圆O直径
所以∠ADP=90°
∴cos∠APD=
sin∠APD=
=
故答案为:
.
所求直线标准方程为x=2,
则极坐标方程为ρcosθ=2.
故答案为:ρcosθ=2.
(2)解:由圆周角定理,可得:
在△ABP和△DCP中
∠A=∠D,∠B=∠C
∴△ABP∽△DCP
所以DP:AP=DC:AB=
| 1 |
| 3 |
连接DA
因为AB是圆O直径
所以∠ADP=90°
∴cos∠APD=
| 1 |
| 3 |
sin∠APD=
| 1-cos2∠APD |
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:(1)本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
(2)本题考查的知识点是圆周角定理,相似三角形的判定与性质,同角三角函数关系,其中利用三角形相似的性质,得到cos∠APD=
,是解答本题的关键.
(2)本题考查的知识点是圆周角定理,相似三角形的判定与性质,同角三角函数关系,其中利用三角形相似的性质,得到cos∠APD=
| 1 |
| 3 |

练习册系列答案
相关题目
 (2007•深圳一模)如图,AB是半圆O的直径,C在半圆上,CD⊥AB于D,且AD=3DB,设∠COD=θ,则
(2007•深圳一模)如图,AB是半圆O的直径,C在半圆上,CD⊥AB于D,且AD=3DB,设∠COD=θ,则