Question

（2012•枣庄一模）如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB，F为CD的中点．
（1）求证：AF∥平面BCE；
（2）求直线BF和平面BCE所成角的正弦值．

Answer 1

分析：（1）设AD=DE=2AB=2a，建立如图所示的空间直角坐标系A-xyz，利用向量的坐标运算得出

AF

=

1

2

(

BE

+

BC)

，AF?平面BCE，AF∥平面BCE．
（2）求出平面BCE的一个法向量

n

，利用

BF

和

n

的夹角求解即可．

解答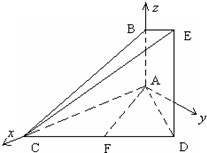：（1）证明：设AD=DE=2AB=2a，建立如图所示的空间直角坐标系A-xyz，则
A（0，0，0），C（2a，0，0），B（0，0，a），D（a，

3

a，0），E（a，

3

a，2a），．
∵F为CD的中点，∴F（

3

2

a，

3

2

a，0）．（2分）

AF

=（

3

2

a，

3

2

a，0）．

BE

=（a，

3

a，a），

BC

=（2a，0，-a），
∵

AF

=

1

2

(

BE

+

BC)

，AF?平面BCE，
∴AF∥平面BCE．
（2）解：设平面BCE的法向量为

n

=（x，y，z），由

n • BE =0 n • BC =0

可得：

x+ 3 y+z=0 2x-z=0

，取x=1，则

n

=（1，

3

，2），（8分）
又

BF

=（

3

2

a，

3

2

a，-a），设BF和平面BCE所成的角为θ，
则sinθ=

| BF • n |

| BF |•| n |

=

2a

2a•2 2

=

2

4

．
∴直线BF和平面BCE所成角的正弦值为

2

4

．（12分）

点评：本题考查直线和平面平行的判定，线面角大小求解．由于本几何体具有良好的建立空间直角坐标系的条件，所以选用了向量方法．可以降低空间想象难度，但要注意计算和关系的转化．