题目内容
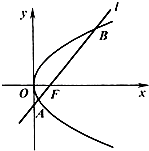 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.(Ⅰ)若线段AB的中点在直线y=2上,求直线l的方程;
(Ⅱ)若|AB|=20,求直线l的方程.
分析:(I)利用“点差法”、中点坐标公式、斜率计算公式即可得出;
(II)设直线l的方程为y=k(x-1),与抛物线方程联立化为k2x2-(4+2k2)x+k2=0,得到根与系数的关系,利用弦长公式|AB|=x1+x2+p即可得到k.
(II)设直线l的方程为y=k(x-1),与抛物线方程联立化为k2x2-(4+2k2)x+k2=0,得到根与系数的关系,利用弦长公式|AB|=x1+x2+p即可得到k.
解答:解:(I)设A(x1,y1),B(x2,y2),线段AB的中点M(x0,2),则x0=
,2=
,kl=
.
由
=4x1,
=4x2,可得(y1+y2)(y1-y2)=4(x1-x2),
∴4kl=4,解得kl=1.
由y2=4x得焦点F(1,0).∴直线l的方程为:y=x-1.
(II)设直线l的方程为y=k(x-1),联立
化为k2x2-(4+2k2)x+k2=0,
∴x1+x2=
.
∵|AB|=x1+x2+p=
+2=10,解得k=±
.
∴直线l的方程为y=±
(x-1).
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| y1-y2 |
| x1-x2 |
由
| y | 2 1 |
| y | 2 2 |
∴4kl=4,解得kl=1.
由y2=4x得焦点F(1,0).∴直线l的方程为:y=x-1.
(II)设直线l的方程为y=k(x-1),联立
|
∴x1+x2=
| 4+2k2 |
| k2 |
∵|AB|=x1+x2+p=
| 4+2k2 |
| k2 |
| ||
| 3 |
∴直线l的方程为y=±
| ||
| 3 |
点评:本题考查了“点差法”、中点坐标公式、斜率计算公式、直线与抛物线相交问题转化为方程联立得到根与系数的关系、弦长公式|AB|=x1+x2+p等基础知识与基本技能方法,属于难题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且
如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且 (2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.
(2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ. (2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.
(2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.