题目内容
数列{an}满足an=2an-1+2n-1(n≥2),其中a3=25.若存在一个实数λ,使得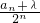 为等差数列,则λ=________.
为等差数列,则λ=________.
-1
分析:由题意求出a3.a2.a1.把表达式两边减去1,然后同除2n,计算 的值,说明数列
的值,说明数列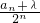 为等差数列,求出λ的值.
为等差数列,求出λ的值.
解答:因为数列{an}满足an=2an-1+2n-1(n≥2),a3=25.a2=9.a1=3.
所以an-1=2an-1-2+2n(n≥2),
所以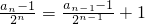 ,
, =3,
=3,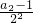 =2,
=2,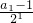 =1,
=1,
所以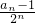 为等差数列,首项为1,公差为1的等差数列.
为等差数列,首项为1,公差为1的等差数列.
所以λ=-1.
故答案为:-1.
点评:本题是中档题,考查数列的递推关系式的应用,注意正确求出数列的通项公式,验证数列是等差数列是解题的关键.
分析:由题意求出a3.a2.a1.把表达式两边减去1,然后同除2n,计算
 的值,说明数列
的值,说明数列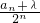 为等差数列,求出λ的值.
为等差数列,求出λ的值.解答:因为数列{an}满足an=2an-1+2n-1(n≥2),a3=25.a2=9.a1=3.
所以an-1=2an-1-2+2n(n≥2),
所以
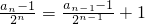 ,
, =3,
=3,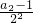 =2,
=2,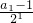 =1,
=1,所以
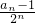 为等差数列,首项为1,公差为1的等差数列.
为等差数列,首项为1,公差为1的等差数列.所以λ=-1.
故答案为:-1.
点评:本题是中档题,考查数列的递推关系式的应用,注意正确求出数列的通项公式,验证数列是等差数列是解题的关键.

练习册系列答案
相关题目