题目内容
 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的离心率;
(2)D是过A,B,F2三点的圆上的点,D到直线l:x-
| 3 |
分析:(1)由题意求出F2(c,0),A(0,b),设B(x0,0),根据向量
⊥
利用数量积建立关系式,算出x0=-
,再由F1为BF2中点化简得a2=4c2,从而求出椭圆C的离心率;
(2)由(1)的结论得到F2、B的坐标,从而得到△ABF2的外接圆圆心为F1(-
a,0),半径r=a.利用点到直线的距离公式,结合题意建立关于a的方程,解之得a=2,进而得到c=1且b=
,可得椭圆C的方程.
| AF2 |
| AB |
| b 2 |
| c |
(2)由(1)的结论得到F2、B的坐标,从而得到△ABF2的外接圆圆心为F1(-
| 1 |
| 2 |
| 3 |
解答:解:(1)设B(x0,0),由F2(c,0),A(0,b),
得
=(c,-b),
=(x0,-b)
∵
⊥
,∴cx0+b2=0,解之得x0=-
,
∵F1为BF2中点,∴-
+c=-2c,化简得b2=3c2=a2-c2,即a2=4c2,
故a=2c,可得椭圆C的离心率e=
=
;
(2)由(1)知c=
a,于是F2(
a,0),B(-
a,0),
△ABF2的外接圆圆心为F1(-
a,0),半径r=a,
∵D到直线l:x-
y-3=0的最大距离等于2a,∴圆心到直线的距离为a,
可得
=a,解之得a=2,得到c=1且b=
,
∴椭圆C的方程为
+
=1.
得
| AF2 |
| AB |
∵
| AF2 |
| AB |
| b 2 |
| c |
∵F1为BF2中点,∴-
| b 2 |
| c |
故a=2c,可得椭圆C的离心率e=
| c |
| a |
| 1 |
| 2 |
(2)由(1)知c=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
△ABF2的外接圆圆心为F1(-
| 1 |
| 2 |
∵D到直线l:x-
| 3 |
可得
|-
| ||
| 2 |
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
点评:本题给出椭圆满足的条件,求椭圆的离心率和方程.着重考查了椭圆的标准方程、简单几何性质和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图,椭圆C:
如图,椭圆C: (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: 如图,椭圆
如图,椭圆 如图,椭圆
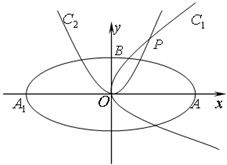
如图,椭圆 (2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:
(2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C: