题目内容
如图,在△ABC中,设BC,CA, AB的长度分别为a,b,c,证明:a2=b2+c2-2bccosA
借助于向量的加法法则和向量的数量积来得到结论。
解析试题分析:证明:设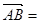 c,
c,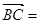 a,
a,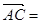 b,则
b,则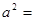 |a|
|a|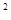 =|
=|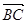 |
|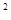 =
=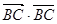
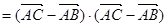
=(b-c)·(b-c)=b·b+c·c-2b·c
=|b|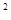 +|c|
+|c|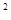 -2|b||c|
-2|b||c|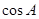 =
=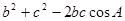
考点:向量的求模运算
点评:解决的关键是把向量表示为向量的差向量,转化为向量的数量积的公式来计算得到结论,属于基础题。

练习册系列答案
相关题目
题目内容
如图,在△ABC中,设BC,CA, AB的长度分别为a,b,c,证明:a2=b2+c2-2bccosA
借助于向量的加法法则和向量的数量积来得到结论。
解析试题分析:证明:设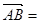 c,
c,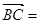 a,
a,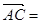 b,则
b,则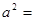 |a|
|a|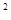 =|
=|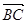 |
|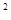 =
=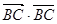
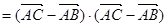
=(b-c)·(b-c)=b·b+c·c-2b·c
=|b|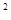 +|c|
+|c|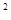 -2|b||c|
-2|b||c|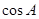 =
=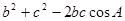
考点:向量的求模运算
点评:解决的关键是把向量表示为向量的差向量,转化为向量的数量积的公式来计算得到结论,属于基础题。
