题目内容
若关于x的方程mx=sin|x|(m>0)在R上恰有3个根,且最小根为α,则有( )
| A、m=tanα | B、m=cosα | C、tanα=α | D、tanα=-α |
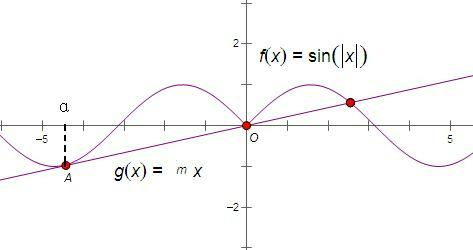
分析:利用直接法解,分别作出函数y=mx和y=sin|x|的图象,欲使原方程恰有3个根,从图象上观察,有3个交点,即直线与曲线的左侧相切,结合导数的意义可解决.
解答:解:分别作出函数y=mx和y=sin|x|的图象,由图知,欲使原方程恰有3个根,从图象上观察,有3个交点,即直线与曲线的左侧y=-sinx相切,设A(α,-sinα),曲线y=-sinx在x=α的导数是-cosα,根据导数的几何意义知,
-cosα=kOA,∴-cosα=kOA=
∴α=tanα.
故选C.
-cosα=kOA,∴-cosα=kOA=
| -sinα |
| α |
故选C.

点评:本题主要考查结合导数的意义、数形结合的思想方法.华罗庚曾说过:“数缺形时少直观,形缺数时难入微.数形结合百般好,隔离分家万事非.”数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目