题目内容
已知函数f(x)=x3-mx+5,x∈R,在x=
处取得极值.
(Ⅰ)过点A(1,0)作曲线y=f(x)的切线,求切线方程.
(Ⅱ)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围.
+ - |
| 2 |
(Ⅰ)过点A(1,0)作曲线y=f(x)的切线,求切线方程.
(Ⅱ)若关于x的方程f(x)=a有3个不同实根,求实数a的取值范围.
分析:(I)求出f'(x),因为函数在x=±
处取得极值,即得到f'(
)=f'(-
)=0,代入求出m得到函数解析式,然后判断点A(1,0)不在曲线上,设切点为M(x0,y0),分别代入导函数和函数中写出切线方程,因为A点在切线上,把A坐标代入求出切点坐标即可求出切线方程.
(Ⅱ)若关于x的方程f(x)=a有3个不同实根,则y=f(x)图象与y=a图象必有3个不同的交点,a应该介于函数的极小值与极大值之间.
| 2 |
| 2 |
| 2 |
(Ⅱ)若关于x的方程f(x)=a有3个不同实根,则y=f(x)图象与y=a图象必有3个不同的交点,a应该介于函数的极小值与极大值之间.
解答:解:(I)f'(x)=3x2-m,依
题意,f'(
)=f'(-
)=0,
即 3(
)2-m=0解得m=6.
∴f(x)=x3-6x+5,曲线方程为y=x3-6x+5,设切点为M(x0,y0),
则点M的坐标满足y0=x03-6x0+5.因f'(x0)=3(x02-2),
故切线的方程为y-y0=3(x02-2)(x-x0)
注意到点A(1,0)在切线上,有0-(x03-6x0+5)=3(x02-2)(1-x0)
解得x0=1或x0=-
.
所以,切点为M(1,0),此时切线方程为y=-3x+3;
或切点为M(-
,
),此时切线方程为y=-
x+
;
(II)对函数f(x)=x3-6x+5求导,得函数f′(x)=3x2-6
令f′(x)>0,即3x2-6>0,解得x>
,或x<-
f′(x)<0,即3x2-6<0,解得-
<x<
f′(x)=0,即3x2-6=0,解得x=
,或x=-
,
f(-
)=5+4
,f(
)=5-4
,
∴f(x)的单调递增区间是(-∞,-
)及(
,+∞),单调递减区间是(-
,
)
当x=-
,f(x)有极大值5+4
;当x=
,f(x)有极小值5-4
当5-4
<a<5+4
时,直线y=a与y=f(x)的图象有3个不同交点,此时方程f(x)=a有3个不同实根.
∴实数a的取值范围为(5-4
,5+4
).
题意,f'(
| 2 |
| 2 |
即 3(
| 2 |
∴f(x)=x3-6x+5,曲线方程为y=x3-6x+5,设切点为M(x0,y0),
则点M的坐标满足y0=x03-6x0+5.因f'(x0)=3(x02-2),
故切线的方程为y-y0=3(x02-2)(x-x0)
注意到点A(1,0)在切线上,有0-(x03-6x0+5)=3(x02-2)(1-x0)
解得x0=1或x0=-
| 1 |
| 2 |
所以,切点为M(1,0),此时切线方程为y=-3x+3;
或切点为M(-
| 1 |
| 2 |
| 63 |
| 8 |
| 21 |
| 4 |
| 21 |
| 4 |
(II)对函数f(x)=x3-6x+5求导,得函数f′(x)=3x2-6
令f′(x)>0,即3x2-6>0,解得x>
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
f(-
| 2 |
| 2 |
| 2 |
| 2 |
∴f(x)的单调递增区间是(-∞,-
| 2 |
| 2 |
| 2 |
| 2 |
当x=-
| 2 |
| 2 |
| 2 |
| 2 |
当5-4
| 2 |
| 2 |
∴实数a的取值范围为(5-4
| 2 |
| 2 |
点评:考查学生利用导数研究函数极值的能力,以及利用导数研究曲线上某点的切线方程的能力,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
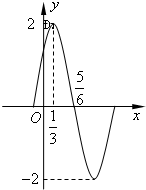 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|