题目内容
【题目】某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设f(n)表示前n年的纯利润总和(f(n)=前n年的总收入﹣前n年的总支出﹣投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方法:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元出售该厂,问哪种方案更合算?
【答案】
(1)解:由题意,第一年共支出12万元,以后每年支出增加4万元,可知每年的支出构成一个等差数列,用g(n)表示前n年的总支出,
∴g(n)=12n+ ![]() ×4=2n2+10n(n∈N*)
×4=2n2+10n(n∈N*)
∵f(n)=前n年的总收入﹣前n年的总支出﹣投资额
∴f(n)=50n﹣(2n2+10n)﹣72=﹣2n2+40n﹣72.
由f(n)>0,即﹣2n2+40n﹣72>0,解得2<n<18
由n∈N*知,从第三年开始盈利.
(2)解:方案①:年平均纯利润为 ![]() =40﹣2(n+
=40﹣2(n+ ![]() )≤16,
)≤16,
当且仅当n=6时等号成立.
故方案①共获利6×16+48=144(万元),此时n=6.
方案②:f(n)=﹣2(n﹣10)2+128.
当n=10时,[f(n)]max=128.
故方案②共获利128+16=144(万元).
比较两种方案,获利都是144万元,但由于方案①只需6年,而方案②需10年,故选择方案①更合算
【解析】(1)根据第一年共支出12万元,以后每年支出增加4万元,可知每年的支出构成一个等差数列,故n年的总支出函数关系可用数列的求和公式得到;再根据f(n)=前n年的总收入﹣前n年的总支出﹣投资额,可得前n年的纯利润总和f(n)关于n的函数关系式;令f(n)>0,并解不等式,即可求得该厂从第几年开始盈利;(2)对两种决策进行具体的比较,以数据来确定那一种方案较好.

 阅读快车系列答案
阅读快车系列答案【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 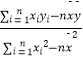 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.