题目内容
（2012•枣庄一模）如图，△ABC中，点D是边BC的中点，E是边AC（靠近点C）的三等分点，则| AP |
| AB |
| AC |
| AP |
| 2 |
| 5 |
| AB |
| AC |
| AP |
| 2 |
| 5 |
| AB |
| AC |
分析：过点E作EF∥AD，交BC于F，在△ADC中利用线段成比例，可得AD=3EF，DF=
CD=
BD．然后在△BEF中利用线段成比例，可得PD=
EF=
AD，所以
=
，结合D是边BC的中点，有
=
（
+
），即可得到本题的答案．
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 5 |
| 1 |
| 5 |
| AP |
| 4 |
| 5 |
| AD |
| AD |
| 1 |
| 2 |
| AB |
| AC |
解答：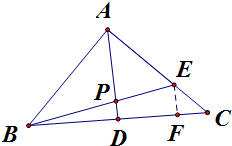
解：过点E作EF∥AD，交BC于F
∵△ADC中，
=
=
=
，∴AD=3EF，DF=
CD=
BD
又∵△BEF中，PD∥EF
∴
=
=
，可得PD=
EF=
AD，
由此可得
=
∵D是边BC的中点，
=
（
+
）
∴
=
×
（
+
）=
（
+
）
故答案为：
=
（
+
）
解：过点E作EF∥AD，交BC于F∵△ADC中，
| EF |
| AD |
| CE |
| AC |
| CF |
| CD |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
又∵△BEF中，PD∥EF
∴
| PD |
| EF |
| BD |
| BF |
| 3 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
由此可得
| AP |
| 4 |
| 5 |
| AD |
∵D是边BC的中点，
| AD |
| 1 |
| 2 |
| AB |
| AC |
∴
| AP |
| 4 |
| 5 |
| 1 |
| 2 |
| AB |
| AC |
| 2 |
| 5 |
| AB |
| AC |
故答案为：
| AP |
| 2 |
| 5 |
| AB |
| AC |
点评：本题给出出三角形的中线和一边的三等分点，求向量
的线性表示式，着重考查了平面向量基本定理和平行线分线段成比例定理等知识，属于中档题．
| AP |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2012•枣庄一模）如图，CDEF是以圆O为圆心，半径为1的圆的内接正方形，将一颗豆子随机地扔到该圆内，用A表示事件“豆子落在扇形OCFH内”（点H将劣弧
（2012•枣庄一模）给定两个长度为1的平面向量