题目内容

中心在原点，焦点在x轴上的双曲线的实轴与虚轴相等，一个焦点到一条渐近线的距离为
2
，则双曲线方程为（　　）
A、x2-y2=1
B、x2-y2=2
C、x2-y2=
2
D、x2-y2=
1
2
分析：由题意，设双曲线方程为
x2
a2
-
y2
a2
=1（a＞0），利用焦点到渐近线的距离等于
2
，求出待定系数 a2 ．
解答：解：由题意，设双曲线方程为
x2
a2
-
y2
a2
=1（a＞0），
则c=
2
a，渐近线y=x，∴
|
2
a|
2
=
2
，∴a2=2．
∴双曲线方程为x2-y2=2．
故选B
点评：本题考查用待定系数法求双曲线的标准方程，以及点到直线的距离公式的应用．
练习册系列答案
相关题目
已知椭圆w的中心在原点，焦点在x轴上，长轴长为4，离心率为
6
3
，△ABC的顶点A，B在椭圆w上，C在直线l：y=x+2上，且AB∥l．
（1）求椭圆w的方程；
（2）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（3）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程．
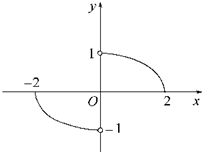精英家教网如图，函数y=f（x）的图象是中心在原点、焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A、{x|-
2
＜x＜0或
2
＜x≤2}
B、{x|-2≤x＜-
2
或
2
＜x≤2}
C、{x|-2≤x＜-
2
2
或
2
2
＜x≤2}
D、{x|-
2
＜x＜
2
，且x≠0}
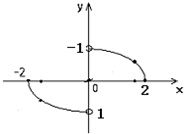精英家教网如图，函数y=f（x）的图象是中心在原点，焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A、{
2
2
＜x≤2或
2
2
＜x≤2}
B、{x|-2≤x＜
2
或
2
＜x≤2}
C、{x|-
2
＜x＜0或
2
＜x≤2}
D、{x|-
2
＜x＜
2
，且x≠0}

（12分）

    已知椭圆中心在原点，焦点在x轴上，长轴长等于12，离心率为.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）过椭圆左顶点作直线l垂直于x轴，若动点M到椭圆右焦点的距离比它到直线l的距离小4，求点M的轨迹方程.

 
已知椭圆w的中心在原点，焦点在x轴上，长轴长为4，离心率为
6
3
，△ABC的顶点A，B在椭圆w上，C在直线l：y=x+2上，且AB∥l．
（1）求椭圆w的方程；
（2）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（3）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网