题目内容
（12分）
已知椭圆中心在原点，焦点在x轴上，长轴长等于12，离心率为
.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）过椭圆左顶点作直线l垂直于x轴，若动点M到椭圆右焦点的距离比它到直线l的距离小4，求点M的轨迹方程.
【答案】
解（Ⅰ）设椭圆的半长轴长为a，半短轴长为b，半焦距为c.
由已知，2a＝12，所以a＝6. （1分）
又
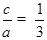，即a＝3c，所以3c＝6，即c＝2. …（3分）[
于是b2＝a2－c2＝36－4＝32. …………………（5分）
因为椭圆的焦点在x轴上，
故椭圆的标准方程是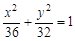
.（6分）
【解析】略
练习册系列答案
相关题目
。