题目内容
4.已知|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=4,$\overrightarrow{a}$与$\overrightarrow{b}$夹角为120°,则向量$\overrightarrow{b}$在向量$\overrightarrow{a}$上的射影为( )| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | 2 | D. | -2 |
分析 利用平面向量的数量积公式得到向量$\overrightarrow{b}$在向量$\overrightarrow{a}$上的射影为:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$.
解答 解:由已知,向量$\overrightarrow{b}$在向量$\overrightarrow{a}$上的射影为:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=|$\overrightarrow{b}|$cos120°=4×(-$\frac{1}{2}$)=-2;
故选D.
点评 本题考查了平没戏了的数量积的几何意义;关键是熟练运用公式.

练习册系列答案
相关题目
15.已知x,y的取值如下表,从散点图可以看出y与x线性相关,且回归方程为$\widehat{y}$=0.95x+a,则a=( )
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A. | 0 | B. | 2.2 | C. | 2.6 | D. | 3.25 |
12.执行如图所示的程序框图,输出的结果( )


| A. | $\frac{3}{4}$ | B. | $\frac{5}{6}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{5}$ |
19.同时投掷两颗骰子,则两颗骰子向上的点数相同的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
9.C${\;}_{6}^{1}$+C${\;}_{6}^{2}$+C${\;}_{6}^{3}$+C${\;}_{6}^{4}$+C${\;}_{6}^{5}$的值为( )
| A. | 64 | B. | 63 | C. | 62 | D. | 61 |
16.已知等差数列{an}的前n项和为Sn,若$\overrightarrow{OB}$=a1 $\overrightarrow{OA}$+a2011$\overrightarrow{OC}$,且A、B、C三点共线(O为该直线外一点),则S2011=( )
| A. | 2011 | B. | $\frac{2011}{2}$ | C. | 22011 | D. | 2-2011 |
12.在△ABC中,已知$\overrightarrow{AB}•\overrightarrow{AC}$=2$\sqrt{3}$,A=60°,则△ABC的面积为( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
 是等差数列,公差
是等差数列,公差 ,
, ,
,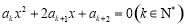 .
. 取不同正整数时,方程都有公共根;
取不同正整数时,方程都有公共根; ,
, ,
,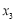 ,…,
,…, ,求证:
,求证: ,
, ,
, ,…,
,…, ,…是等差数列.
,…是等差数列.